Question 1179761: The sum of two whole numbers is 29. find the maximum possible product of the two numbers.
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! Let one number x and the other one y.
x + y = 29
The product of the two numbers will be x * y = xy
solve x + y = 29
y = 29 - x
x * y = x(29 - x) = 29x - x²
let f(x)= 29x-x^2,
f'(x) = 29 - 2x
The maximum value of this function will occur at a critical number. A critical number occurs where f'(x) = 0 or is undefined.
f'(x) is defined for all real x.
We only need to determine where f'(x) = 0
29 - 2x = 0
29 = 2x
x = 14.5
The two numbers are 14.5 ,14.5
Answer by ikleyn(52816)  (Show Source):
You can put this solution on YOUR website! .
Surely, the answer by @mananth is incorrect:
the problem asks about INTEGER numbers, while his / (her) answer is non-integer.
If x is one number, then the other number is 29-x.
Their product is x*(29-x) = 29x - x^2. (1)
This function is a parabola placed downward.
29x - x^2 = 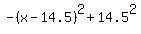 . (2)
The parabola has the vertex at x = 14.5.
From the formula (2), it is clear, that our integer numbers are those that are closest to 14.5.
These numbers are 14 and 15.
So, there are two pairs of the numbers that give the answer: (14,15) and (15,14).
Their product is 14*15 = 210 = 15*14.
Solved and explained.
|
|
|
