SOLUTION: The graph of a quadratic function passes through (-2, 4) and has vertex (1, -6). Use symmetry to identify one other point that must be on the graph of this function.

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: The graph of a quadratic function passes through (-2, 4) and has vertex (1, -6). Use symmetry to identify one other point that must be on the graph of this function.      Log On


   

Question 1179756: The graph of a quadratic function passes through (-2, 4) and has
vertex (1, -6).
Use symmetry to identify one other point that must be on the
graph of this function.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!

Hi
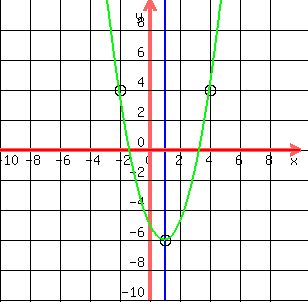
the vertex form of a Parabola opening up(a>0) or down(a<0), 
y=a%28x-h%29%5E2+%2Bk 
where(h,k) is the vertex  and  x = h  is the Line of Symmetry 
Question States:  y = a(x-1)^2 - 6  x = 1 line of symmetry

P(-2,4) and P(4,4) are both 3 from the line of symmetry.

Wish You the Best in your Studies.
y = (10/9)(x-1)^2  - 6