Question 11793: It has been 17 years since I have taken Algebra and now I am taking College Algebra. My instructor has given several problems that I can't figure out.
1) Find the slope-intercept form of the equation of the line through the point (-5,-3), parallel to the line 7x-6y=-1.
My work:
y=mx+b
7x-6y=-1
7x-6y=-1
-6y=-7x-1
y=7/6x+6
How do I coplete the problem?
Thanks
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! Your first step is correct. You need to take the given equation of the line in standard form, and convert it to slope-intercept form, in order to find the slope of the given line.
7x-6y=-1
7x-6y=-1
-6y=-7x-1
y=7/6x+6
According to this, the slope of the given line is  , so the slope of the line parallel to this line is ALSO  .
There are two ways to go from here. I recommend using the simplest formula you can here (y=mx+b), and substitute in the values that you know: m=, and x=-5 and y = -3, and solve for b.
y = mx + b
To clear the ugly fraction, it's nice to multiply both sides by 6:
 Divide out the 6 on the right side of the equation:
Add + 35 to each side:
Divide both sides by 6:
Remember what b represents? The y-intercept, so the final answer is:
As a check, let x = -5, substitute into this equation, and see if you get y = -3:
 =  = 
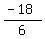It checks.
This may not be the most common method to solve this, but I think it's the easiest method!
R^2 at SCC
|
|
|
