Question 117895: I hope I am posting this in the correct place. I am really stuck on this and do not know what to do. Please help me understand how to do this, Thank you so much.
2{[3(m-5)+18]-[3(5m-3)+4]}
Found 3 solutions by Earlsdon, solver91311, Edwin McCravy:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2{[3(m-5)+18]-[3(5m-3)+4]} Start by applying the "distributive property" to the inner-most parentheses.
2{[(3m-15)+18]-[(15m-9)+4]} Now you can remove the inner-most parentheses and simplify the inner backets ([...])
2{[3m-15+18}-[15m-9+4]}
2{[3m+3]-[15m-5]} Remove the brackets and simplify inside the curly brackets ({...})
2{3m+3-15m+5}
2{3m-15m+3+5}
2{-12m+8} Finally, apply the distibutive property.
-24m+16
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 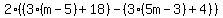
This is just an exercise in the application of the Distributive, Associative, and Commutative Properties:
Distributive Property:  for all real a, b, and c. for all real a, b, and c.
Associative Property:  for all real a, b, and c. for all real a, b, and c.
Commutative Property:  for all real a and b. for all real a and b.
For this problem you need to work from the inside and go out. Start with the 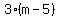 part. Using the distributive property, you can write that as part. Using the distributive property, you can write that as  . Same thing for the . Same thing for the 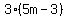 part, which can be written as part, which can be written as 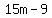 . Put these two expressions back into the original expression: . Put these two expressions back into the original expression:
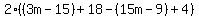
Now remove the parentheses around  by distributing the minus sign. Think of the minus sign in front of a set of parentheses as a -1, and then apply the distributive property. You end up with by distributing the minus sign. Think of the minus sign in front of a set of parentheses as a -1, and then apply the distributive property. You end up with 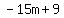 . Put this back into the expression. . Put this back into the expression.
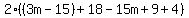
Next you can remove the parentheses from the 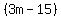 without changing anything else because there is no minus sign in front of this quantity. without changing anything else because there is no minus sign in front of this quantity.
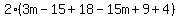
For the expression that is still inside of the parentheses, you have 2 terms that contain the variable m, and 4 terms that are just numbers. Add up all the like terms so that you get  and and 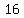 . This is where we are applying the Associative and Commutative Properties. . This is where we are applying the Associative and Commutative Properties.
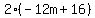
One last application of the Distributive Property and we are done:
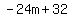 , or it might be more neatly put , or it might be more neatly put 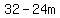
Hope that helps. I hope you and your family have a joyous holiday season.
John
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
2{[3(m-5)+18]-[3(5m-3)+4]}
First look for the first innermost pair of grouping symbols.
That is, grouping sysmbols which have no grouping symbols
between them. So we see (m-5).
Then we ask: "Is there anything which we can do with what is
inside " m-5 ".
The answer is no.
Then we ask: "How do we remove those grouping symbols around
" m-5 "?"
The answer is by distributing the 3 just outside the (m-5),
getting 3m-15, so in place of 3(m-5) we write 3m-15, and
copy everything else over, getting
2{[3m-15+18]-[3(5m-3)+4]}
-----------------------------------------
Now we start over. Look for the first innermost pair of
grouping symbols. That is, grouping sysmbols which have
no grouping symbols between them. So we see [3m-15+18].
Then we ask: "Is there anything which we can do with what is
inside "3m-15+18".
The answer is yes, we can combine the -15 and the +18 getting
"3m+3". So we replace "3m-15+18" by "3m+3", and copy
everything else over:
2{[3m+3]-[3(5m-3)+4]}
---------------------------------------
Now we start over. Look for the first innermost pair of
grouping symbols. That is, grouping sysmbols which have
no grouping symbols between them. So we see [3m+3].
Then we ask: "How do we remove those grouping symbols around
3m+3?"
The answer is by putting the invisible 1 just left of [3m+3],
like this:
2{1[3m+3]-[3(5m-3)+4]}
and distributing the 1 just outside the [3m+3],
getting 3m+3, so in place of [3m+3] we write 3m+3, and
copy everything else over, getting
2{3m+3-[3(5m-3)+4]}
---------------------------------------
Now we start over again. Look for the first innermost pair of
grouping symbols. That is, grouping symbols which have
no grouping symbols between them. So we see (5m-3).
Then we ask: "Is there anything which we can do with what is
inside, that is, "5m-3".
The answer is no.
Then we ask: "How do we remove those grouping symbols around
" 5m-3 "?
The answer is by distributing the 3 just outside the (5m-3),
getting 15m-9, so in place of 3(5m-3) we write 15m-9, and
copy everything else over, getting
2{3m+3-[15m-9+4]}
--------------------------------------------
Once more, we start over. Look for the first innermost pair
of grouping symbols. That is, grouping sysmbols which have
no grouping symbols between them. So we see [15m-9+4].
Then we ask: "Is there anything which we can do with what is
inside, namely, "15m-9+4".
The answer is yes. The answer is yes, we can combine the -9
and the +4 getting "15m-5". So we replace "15m-9+4" by "15m-5",
and copy everything else over:
2{3m+3-[15m-5]}
-----------------------------
Once more, we start over. Look for the first innermost pair
of grouping symbols. That is, grouping sysmbols which have
no grouping symbols between them. So we see [15m-5].
Then we ask: "Is there anything which we can do with what is
inside, namely, "15m-5".
The answer is no.
Then we ask: "How do we remove those grouping symbols around
15m-5?"
The answer is by putting the invisible 1 just left of [15m-5],
like this:
2{3m+3-1[15m-5]}
and distributing the -1 just outside the [15m-5],
getting -15m+5, so in place of -1[15m-5] we write -15m+5, and
copy everything else over, getting
2{3m+3-15m+5}
--------
Now we start over again. Look for the first innermost pair of
grouping symbols. That is, grouping symbols which have
no grouping symbols between them. So we see {3m+3-15m+5}.
Then we ask: "Is there anything which we can do with what is
inside, namely " 3m+3-15m+5 ".
The answer is yes, we can combine the 3m and the -15m, and also
the +3 and the +5, getting "-12m+8". So we replace "3m+3-15m+5"
by "-12m+8", and copy everything else over:
2{-12m+8}
---------------------------------------
Starting over again, we look for the first innermost pair of
grouping symbols. That is, grouping sysmbols which have no
grouping symbols between them. So we see {-12m+8}.
Then we ask: "Is there anything which we can do with what is
inside, namely, " -12m+8 ".
The answer is no.
Then we ask: "How do we remove those grouping symbols around
" -12m+8 "?"
The answer is by distributing the 2 just outside the {-12m+8},
getting -24m+16, so in place of 2{-12m+8} we write -24m+16.
There are no grouping symbols and nothing else can be done with
-24m+16, so we are done.
The answer is -24m+16.
Edwin
|
|
|