Question 1178933: if tan(a) = -2, find the exact value of sin(a) and specify each possible quadrant
Found 4 solutions by MathLover1, ewatrrr, ikleyn, MathTherapy:
Answer by MathLover1(20850)   (Show Source):
Answer by ewatrrr(24785)  (Show Source):
You can put this solution on YOUR website! (cos,sin) Unit Circle
Note: sin(a) can have a negative value in III and IV Quadrants
However, in this case:
tan=sin/cos: is negative,
(A -sin and +cos only happens in the 4th quadrant)
 .
Answer by ikleyn(52824)  (Show Source):
You can put this solution on YOUR website! .
If at the test you will solve the problem as @MathLover1 does it and teaches you,
the unsatisfactory score is GUARANTEED to you,
because the solution by @MathLover1 is INCORRECT.
I came to bring you the correct solution.
tan(a) = -2 means that the angle "a" is in the second quadrant, QII, OR in the fourth quadrant, QIV.
tan(a) = -2 means that the opposite leg of the right angled triangle has the length 2, while the adjacent leg is of the length 1.
It implies that the hypotenuse is 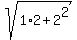 =  units long, and therefore
|sin(a)| =  .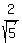
Now we should determine THE SIGN of sin(a).
There are TWO CASES, and we should consider them SEPARATELY.
CASE 1. Angle "a" is in QII
in this case, sin(a) is positive, hence sin(a) = =  .
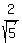CASE 2. Angle "a" is in QIV
in this case, sin(a) is negative, hence sin(a) =  =  .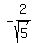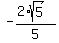
ANSWER. If tan(a) = -2, then there are two possibilities for "a" and for sin(a).
If angle "a" is in QII, then sin(a) = = .
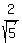If angle "a" is in QIV, then sin(a) =  =  .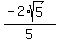
Solved (correctly, as it SHOULD BE); answered and explained. And completed.
-------------
For your safety, ignore the post by @MathLover1.
Also, ignore the post by @ewatrrr, since it is IRRELEVANT to the right solution.
////////////
At this forum, there is a group of reasonable tutors, who know the subject, are competent in Math and can teach ADEQUATELY.
At the same time, there is a group of tutors (I call them "quasi-tutors" and "pseudo-tutors"),
that don't know the subject, are not competent and can not teach adequately.
You, the visitor, should know it --- it is the truth of the life.
It is life ---- or, as the Frenchs say, "c'est la vie".
Answer by MathTherapy(10555)  (Show Source):
|
|
|
