|
Question 1178875: I don't really know how to solve this question so I could use some help.
There are about 3 million births per year in a certain country and about 4800 hospitals. The births over a ten year period are evenly distributed over all the hospitals. Suppose each of the hospitals divided their births into strings of 19 consecutive births. Assume that boy and girl births are equally likely.
a) What is the probability of 19 births in a row being boys?
b) What is the probability, in any one of the hospitals of having a string of all boys?
c) Based on the answer to part b, what is the probability that at least one of the 4800 hospitals would have a string of all boys?
Here is what I have tried so far but I don't think that it is correct.
a) 0.5 ^ 19 = 1.907 X 10 ^-6
0.5 because there is 1/2 chance of a boy birth and 1/2 chance of girl birth
19 because there are a string of 19 boys
I am not really sure how to solve the other questions.
Answer by Solver92311(821)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your answer to part a) is spot on.
^{19}(0.5)^0)
Which reduces to
^{19}\cdot\,1\ \approx\ 1.907E-6)
as you reported.
Since your set up said "about 3 million" births in 4800 hospitals, I'm going to make it 3,009,600 births in 4800 hospitals which means 627 births per hospital and 33 sets of 19 births per hospital.
So your part b wants the probability of one hospital, i.e. 33 sets of 19 births, to have a string of 19 boys out of 33 tries. The thing is, any number of sets of 19 boys from 1 to 33 would qualify. So what you want is the probability that in any one hospital what is the probability of at least one set of 19 boys. Straight up, this is a seriously ugly mess of arithmetic because you need to compute, where 
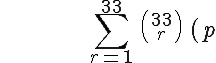^r(1-p)^{33-r})
Which would require computing 33 terms and then summing them all. However, we can simplify the computation considerably by considering the fact that the probability of something happening at least once is equal to 1 minus the probability that it doesn't happen at all. For this situation:
\ =\ 1\ -\ {{33}\choose{0}}\cdot(p)^0(1-p)^{33}\ =\ 1\cdot\ 1\cdot (1-p)^{33})
For part c), I'll refer to the result of part b as 
Again we are faced with an "at least" situation, so we need to compute 1 minus the probability that it doesn't happen at all, in other words, 1 minus the probability of zero successes in 4800 trials where the probability of success on any given trial is 
\ =\ 1\ -\ {{4800}\choose{0}}\cdot(p_1)^0(1-p_1)^{4800}\ =\ 1\cdot\ 1\cdot (1-p_1)^{4800})
You can do your own arithmetic.
John

My calculator said it, I believe it, that settles it

From
I > Ø

|
|
|
| |