Question 1178846: If 
Then find the value of
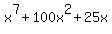
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52818)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If x^3 + 5x - 10 = 0, then find the value of x^7 + 100x^2 + 25x.
~~~~~~~~~~~~~~~
From x^3 + 5x - 10 = 0 we express
x^3 = 10-5x. (1)
Next, we consider x^7 and will transform it step by step, decreasing the degree of x,
replacing x^3 at each appearance by (10-5x), according to (1)
x*7 = x^4 * x^3 = x^4 * (10-5x) = 10x^4 - 5x^5 = 10x*x^3 - 5x^2*x^3 =
= 10x*(10-5x) - 5x^2*(10-5x) = 100x - 50x^2 - 50x^2 + 25x^3 =
= 100x - 100x^2 + 25*(10-5x) = 100x - 100x^2 + 250 - 125x = -100x^2 - 25x + 250. (2)
Now x^7 + 100x^2 + 25x = substitute expression (2) instead of x^7 =
= (-100x^2 - 25x + 250) + 100x^2 + 25x = combine like terms = 250.
ANSWER. If x^3 + 5x - 10 = 0, then x^7 + 100x^2 + 25x = 250.
Solved.
---------------
It looks like a trick, a focus, but, actually, it is THE METHOD.
In mathematical language, it is called "decreasing a degree", or "lowering a degree".
We systematically use expression (1), x^3 = 10-5x, to decrease the degree of x^7, step by step.
Having this expression (1), it allows us to run/(to start)/(to launch) the "decreasing a degree" engine.
//////////////
Do not forget to post your "THANKS" to me for my teaching.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given: x^3+5x-10=0
Rewrite as x^3=10-5x, and also as x^3+5x=10
Square both sides in the first of those: x^6=100-100x+25x^2
Multiply by x: x^7=100x-100x^2+25x^3
Use that to evaluate the expression we are to evaluate:
x^7+100x^2+25x = 100x+25x^3+25x = 125x+25x^3 = 25(x^3+5x) = 25(10) = 250
ANSWER: 250
|
|
|