Question 1178826: A bin contains 75 light bulbs, 5 of which are defective. If 5 light bulbs are randomly selected from the bin with replacements, find the probability that all the bulbs selected are good. Round to three decimal places as needed. What equation would I use to find the answer?
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It means that you, actually, select your bulbs from the set of 70 good bulbs.
Therefore, you may find the probability as
P = 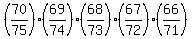 = 0.70124 (rounded). ANSWER
The formula says that you first select any of 70 good bulbs from the total of 75 bulbs;
then you select any of 69 remaining good bulbs from the total of remaining 74 bulbs;
. . . and so on 5 times, in all, completing your selection.
If you are familiar with the notion/conception of COMBINATIONS, you may write the formula for probability in this way
P = = 0.70124 (rounded). ANSWER
The formula says that you first select any of 70 good bulbs from the total of 75 bulbs;
then you select any of 69 remaining good bulbs from the total of remaining 74 bulbs;
. . . and so on 5 times, in all, completing your selection.
If you are familiar with the notion/conception of COMBINATIONS, you may write the formula for probability in this way
P = 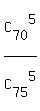 ,
which says that the total space of events contains ,
which says that the total space of events contains 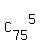 elements,
while the space of favorable events has elements,
while the space of favorable events has 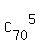 elements.
Both formulas produce the same value and the same answer. elements.
Both formulas produce the same value and the same answer.
Your problem/question is solved, answered, explained and completed.
----------------
To learn the subject better by examples, look into the lessons
- Elementary Probability problems related to combinations
- Elementary Probability problems related to combinations REVISITED
in this site.
You will find a variety of similar (and different) solved problems there (!)
|
|
|