SOLUTION: Please help me solve this! Use properties of logarithms to expand the logarithmic expression as much as possible. Where​ possible, evaluate logarithmic expressions without us

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Please help me solve this! Use properties of logarithms to expand the logarithmic expression as much as possible. Where​ possible, evaluate logarithmic expressions without us      Log On


   

Question 1178811: Please help me solve this!
Use properties of logarithms to expand the logarithmic expression as much as possible. Where​ possible, evaluate logarithmic expressions without using a calculator.
log+%2810x%5E4+3sqrt%285-x%29%2F3%28x%2B6%29%5E2%29
The top row is 10x%5E4 next to the sqrt not 43 as it appears. Thanks so much!
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
I think you meant CUBE root, not SQUARE root, so use "root(3,5-x)" not sqrt.

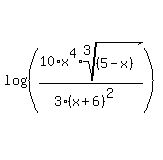log%28%2810%2Ax%5E4%2Aroot%283%2C%285-x%29%29%2F%283%28x%2B6%29%5E2%29%29%29

That's the log of a quotient, so we use log%28%28a%2Fb%29%29=log%28%28a%29%29-log%28%28b%29%29

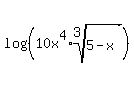
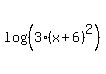log%28%2810x%5E4%2Aroot%283%2C5-x%29%29%29%22%22-%22%22log%28%283%28x%2B6%29%5E2%29%29

Those are both logs of products, so we use log%28%28abc%29%29=log%28%28a%29%29%2Blog%28%28b%29%29%2Blog%28%28c%29%29 on the first log:

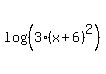log%28%2810%29%29%2Blog%28%28x%5E4%29%29%2Blog%28%28root%283%2C%285-x%29%29%29%29%22%22-%22%22log%28%283%28x%2B6%29%5E2%29%29

Now we must be careful to put a big parentheses around the second log's
break-up since it's preceded by a minus:

log%28%2810%29%29%2Blog%28%28x%5E4%29%29%2Blog%28%28root%283%2C%285-x%29%29%29%29%22%22-%22%22%28log%28%283%29%29%2Blog%28%28%28x%2B6%29%5E2%29%29%29

Now we can remove that big parentheses by changing the signs of the terms
inside the big parentheses:



Now we write the cube root as the 1/3 power:



Now we use log%28%28a%5Eb%29%29=b%2Alog%28%28a%29%29 and also log(10) = 1:



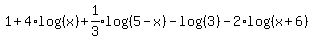Edwin