Question 1178775: In a 2019 poll of adults 18 years and older, (BBMG Conscious Consumer Report)
about half of them said that despite tough economic times, they are willing to pay
more for products that have social and environmental benefits. Suppose that 50% of
all such adults currently hold this view. Find the probability that in a random sample
of 20 such adults, the number of adults in this sample who hold this opinion is:
a. none [2 marks]
b. exactly 10 [2 marks]
c. at most 7 [2 marks]
d. more than 10 [3 marks]
e. at least 13 [3 marks]
f. 12 to 15 (inclusive) [3 marks]
Answer by ikleyn(52814)   (Show Source):
You can put this solution on YOUR website! .
In a 2019 poll of adults 18 years and older, (BBMG Conscious Consumer Report)
about half of them said that despite tough economic times, they are willing to pay
more for products that have social and environmental benefits. Suppose that 50% of
all such adults currently hold this view. Find the probability that in a random sample
of 20 such adults, the number of adults in this sample who hold this opinion is:
a. none
b. exactly 10
c. at most 7
d. more than 10
e. at least 13
f. 12 to 15 (inclusive)
~~~~~~~~~~~~~~~
All these questions are about binomial distribution probability problems.
In all these cases you need calculate the probability P(n,k,p), where
- number of trials n = 20;
- Probability of success on a single trial p = 0.5;
- k is the number of success trials, which varies from case to case.
To facilitate calculations, I use an online (free of charge) calculator at this web-site
https://stattrek.com/online-calculator/binomial.aspx
It provides nice instructions and a convenient input and output for all relevant options/cases.
(a) "none" means 0 (zero) susccessful trials k=0.
So, in this case you need calculate P(n=20; k=0; p=0.5).
The calculators gives P(n=20; k=0; p=0.5) = 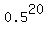 = 9.53674E-07. ANSWER
(b) In this case you need calculate P(n=20; k=10; p=0.5).
The calculators gives P(n=20; k=10; p=0.5) = 0.1762 (rounded). ANSWER
(c) In this case you need calculate P(n=20; k<=7; p=0.5).
The calculators gives P(n=20; k<=7; p=0.5) = 0.1316 (rounded). ANSWER
(d) In this case you need calculate P(n=20; k>10; p=0.5).
* * * Do it ON YOUR OWN, as instructed. * * *
(e) In this case you need calculate P(n=20; k>=13; p=0.5).
* * * Do it ON YOUR OWN, as instructed. * * *
At this point, I stop my teaching.
--------------
Do not forget to post your "THANKS" to me (!)
///////////////
To see a variety of similar solved problems, look into the lessons
- Simple and simplest probability problems on Binomial distribution
- Typical binomial distribution probability problems
- How to calculate Binomial probabilities with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using MS Excel)
- Solving problems on Binomial distribution with Technology (using online solver)
in this site.
After reading these lessons, you will be able to solve such problems on your own,
which is your PRIMARY MAJOR GOAL visiting this forum (I believe).
|
|
|
