Question 117873: A ball is thrown upward from the roof of a building 100 m tall with an initial velocity of 20 m/s.
When will the ball reach a height of 80 m?
Found 2 solutions by MathLover1, solver91311:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are starting at a height of 100 meters, so in order for the ball to reach a height of 80 meters, you are going to have to throw the ball up in such a way that it falls back past the edge of the roof and continues down toward the ground.
The formula for distance traveled by an object with an initial velocity and a constant acceleration (gravity applies a constant -- relatively speaking -- force to the ball) is:

Where a is the constant acceleration, 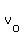 is the initial velocity, is the initial velocity, 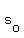 is the initial distance, and t is the time. is the initial distance, and t is the time.
Since the problem givens are in meters and meters/sec, we need the gravitational acceleration constant from the mks system of measurement. This constant, expressed precisely enough for this problem, is 9.8 m/
Remember, velocity and acceleration are vector quantities. They have both magnitude and direction. Since we are throwing the ball up, let's make the initial velocity a positive quantity. But the acceleration vector, the acceleration due to gravity, is acting in the opposite direction, so that quantity must be negative. Finally, since we are starting at the top of a 100 meter building, i.e. we are 100 meters above the ground, that quantity should be positive.
Let's express what we know symbolically:

Giving us an expression for s as a function of time in seconds, time zero being the instant the thrown ball leaves your hand.
We want to know what the time will be when  . So let's write: . So let's write:

Giving us a quadratic equation that can be solved for t.

Apply the quadratic formula:


 or or

A little work with the calculator shows us that  is approximately -0.8 seconds. Since time 0 is when you actually threw the ball, a negative time value doesn't make any sense for this problem, so we can exclude the is approximately -0.8 seconds. Since time 0 is when you actually threw the ball, a negative time value doesn't make any sense for this problem, so we can exclude the  solution. solution.
The calculator then shows us that  is a little less than 5 seconds (4.912...). Because the givens in the problem were all expressed to whole number precision, the appropriate precision for your answer is to the nearest second. Therefore, the answer is 5 seconds. is a little less than 5 seconds (4.912...). Because the givens in the problem were all expressed to whole number precision, the appropriate precision for your answer is to the nearest second. Therefore, the answer is 5 seconds.
General Rule: When you are asked to make calculations based on measurements, the precision of your answer can never be greater than the LEAST precise measurement given. Example: Let's say you are asked to find the area of a rectangle with sides 1 meter and 1.43758 meters. The appropriate answer is 1 square meter, because the least precise measurement given was to the nearest meter. On the other hand, if the measurements for the same problem had been given as 1.00 meters and 1.43758 meters, the correct answer would be 1.44 square meters -- rounded to the nearest 100th meter because the least precise measurement, 1.00, was expressed to two digit precision. Note that 1 meter and 1.00 meters are NOT the same thing at all. Saying 1 meter means that the actual length could actually be anywhere between 0.5 meters and 1.49999... meters, whereas 1.00 meters means that the actual length must be at least 0.95 meters and less than but not equal to 1.05 meters.
The point being that if you express the answer to this question as 4.9 or 4.91 or 4.912, ad infinitum, you are technically wrong. Furthermore, no matter how many decimal places you use, you can never express the exact answer because the exact answer, 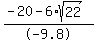 , is an irrational number. 5 seconds is the only correct numerical approximation of the answer. , is an irrational number. 5 seconds is the only correct numerical approximation of the answer.
Hope that helps.
Happy holidays to you and your family
John
|
|
|