Question 1178407: the corner of a triangular base of a truncated prism is defined by A, B, and C. what is its volume if the length of AB =10 ft, BC = 9ft and CA is 12 ft. the sides at A, B and C are perpendicular to the triangular base and have the height of 8.6 ft, 7.1 ft and 5.5 ft, respectively.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
the  vertices of a triangular base of a truncated prism is defined by A, B, and C. vertices of a triangular base of a truncated prism is defined by A, B, and C.
what is its volume if the length of AB =10 ft, BC = 9ft and CA is 12 ft.
the sides at A, B and C are perpendicular to the triangular base and have the height
of 8.6 ft, 7.1 ft and 5.5 ft, respectively.
~~~~~~~~~~~~~~~
The volume of a truncated triangular prim is
V = 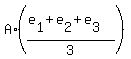 ,
where A the area of a right section (the base) and e1, e2 e3 are the lengths of the lateral edges.
So, calculate the base area using the Heron's formula and given base edges 10 ft, 9 ft and 12 ft.
You may use this online calculator
https://keisan.casio.com/exec/system/1223267646
It will give you the base area of 44.039 ft^2.
Then multiply this area by ,
where A the area of a right section (the base) and e1, e2 e3 are the lengths of the lateral edges.
So, calculate the base area using the Heron's formula and given base edges 10 ft, 9 ft and 12 ft.
You may use this online calculator
https://keisan.casio.com/exec/system/1223267646
It will give you the base area of 44.039 ft^2.
Then multiply this area by 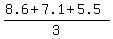 = 7.066 ft.
You will get the volume of your truncated prism of V = 44.039 * 7.066 = 311.17 ft^3. ANSWER = 7.066 ft.
You will get the volume of your truncated prism of V = 44.039 * 7.066 = 311.17 ft^3. ANSWER
Solved.
|
|
|