.
The solution by @MathLover1 is wrong.
If you solve such problem at exam this way, unsatisfactory score is guaranteed to you.
Therefore, I came to bring a correct solution.
From  = 3 you have two cases.
a)
= 3 you have two cases.
a)  =
=  , and
b)
, and
b)  = -
= -  .
Let's consider these cases separately.
a)
.
Let's consider these cases separately.
a)  =
=  .
Then
.
Then 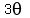 = 30° or
= 30° or 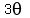 = 210°;
but since the problem talks about
= 210°;
but since the problem talks about 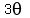 , you must consider
also the angles 30° + 360° = 390° and 30° + 720° = 750°;
as well as the angles 210°+ 360° = 570° and 210°+ 720° = 930°.
These 6 angles for
, you must consider
also the angles 30° + 360° = 390° and 30° + 720° = 750°;
as well as the angles 210°+ 360° = 570° and 210°+ 720° = 930°.
These 6 angles for 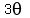 , 30°, 390°, 750°, 210°, 570° and 930°,
give 6 different angles for
, 30°, 390°, 750°, 210°, 570° and 930°,
give 6 different angles for  : 10°, 130°, 250°, 70°, 190° and 310°.
b) Similarly for
: 10°, 130°, 250°, 70°, 190° and 310°.
b) Similarly for  = -
= -  .
Then
.
Then 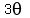 = 150° or
= 150° or 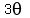 = 330°;
but since the problem talks about
= 330°;
but since the problem talks about 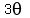 , you must consider
also the angles 150° + 360° = 510° and 150° + 720° = 870°;
as well as the angles 330° + 360° = 690° and 330° + 720° =1050°.
These 6 angles for
, you must consider
also the angles 150° + 360° = 510° and 150° + 720° = 870°;
as well as the angles 330° + 360° = 690° and 330° + 720° =1050°.
These 6 angles for 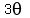 , 150°, 510°, 870°, 330°, 690° and 1050°,
give 6 different angles for
, 150°, 510°, 870°, 330°, 690° and 1050°,
give 6 different angles for  : 50°, 170°, 290°, 110°, 230° and 350°.
Finally, these 6 + 6 = 12 angles gives you the full
ANSWER. 10°, 130°, 250°, 70°, 190° and 310°,
50°, 170°, 290°, 110°, 230° and 350°.
: 50°, 170°, 290°, 110°, 230° and 350°.
Finally, these 6 + 6 = 12 angles gives you the full
ANSWER. 10°, 130°, 250°, 70°, 190° and 310°,
50°, 170°, 290°, 110°, 230° and 350°.
Solved (correctly).