Question 1178200: What nominal rate of interest compounded quarterly is needed to triple a principle in 9 years? (Round your answer to 2 decimal places)
A=P(1+r)^t
4=1(1+r)^9
4=1+r^9
4-1=r^9
3=r^9
I saw this formula online: A=P(1+r)^t. I saw that there are similar problems posted on this site, and I see that they use "log," but I can not find an example that shows the complete steps. Also, do you have to use log to solve this?
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your starting equation is INCORRECT.
The standard translation of the words to Math is THIS equation
3P = 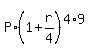 , (1)
where P is the principle amount, r is the nominal annual rate of interest presented as decimal.
4 is the number of quarters in an year and 9 is the number of years.
Canceling P in both sides, you get this equation
3 = , (1)
where P is the principle amount, r is the nominal annual rate of interest presented as decimal.
4 is the number of quarters in an year and 9 is the number of years.
Canceling P in both sides, you get this equation
3 = 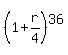 (2)
with one unknown "r".
The standard method to solve it is to take logarithm of both sides.
It gives
log(3) = 36*log(1+r/4), (2)
with one unknown "r".
The standard method to solve it is to take logarithm of both sides.
It gives
log(3) = 36*log(1+r/4),
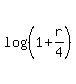 = = 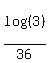 = 0.013253 = 0.013253
 = 10^0.013253 = 1.030987, = 10^0.013253 = 1.030987,
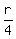 = 1.030987 - 1 = 0.030987
r = 4*0.30987 = 0.123948 = 0.124 (rounded) = 12.4%. ANSWER
ANSWER. The nominal annual percentage rate is 12.4%.
The nominal decimal annual rate is 0.124.
CHECK. = 1.030987 - 1 = 0.030987
r = 4*0.30987 = 0.123948 = 0.124 (rounded) = 12.4%. ANSWER
ANSWER. The nominal annual percentage rate is 12.4%.
The nominal decimal annual rate is 0.124.
CHECK. 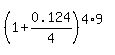 = use your calculator = 3.00. ! Correct !. = use your calculator = 3.00. ! Correct !.
Solved.
------------
You can solve equation (2) differently, by taking the root of degree 36 of both sides.
You will get then
 = 3^(1/36) = 1.030987
which leads you to the same final answer for "r". = 3^(1/36) = 1.030987
which leads you to the same final answer for "r".
-------------
To see many other similar (and different) solved problems, look into the lessons
- Compound interest percentage problems
- Problems on discretely compound accounts
in this site, and learn the subject from there.
After reading these lessons, you will tackle such problems on your own without asking for help from outside.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Happy learning (!)
|
|
|