SOLUTION: Solve the equation for exact solutions in the interval 0 ≤ x < 2𝜋. sin 4x − sqrt3 sin 2x = 0

Algebra ->  Trigonometry-basics -> SOLUTION: Solve the equation for exact solutions in the interval 0 ≤ x < 2𝜋. sin 4x − sqrt3 sin 2x = 0      Log On


   

Question 1178162: Solve the equation for exact solutions in the interval 0 ≤ x < 2𝜋.
sin 4x − sqrt3 sin 2x = 0
Found 3 solutions by greenestamps, Edwin McCravy, ikleyn:
Answer by greenestamps(13215) About Me  (Show Source):
You can put this solution on YOUR website!


sin%284x%29-sqrt%283%29%2Asin%282x%29=0

The arguments for sine are 4x and 2x. Use the double angle formula for sine to represent sin(4x) in terms of sin(2x) and cos(2x).

2sin%282x%29cos%282x%29-sqrt%283%29%2Asin%282x%29=0

Factor (the terms have a common factor of sin(2x))

sin%282x%29%282cos%282x%29-sqrt%283%29%29=0
sin%282x%29=0 OR 2cos%282x%29-sqrt%283%29=0

I'll leave it for you to finish from there.

Re-post, showing the work you have done, if you need more help.

Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
sin%284x%29+%E2%88%92+sqrt%283%29sin%282x%29+=+0

2sin%282x%29cos%282x%29+-+sqrt%283%29sin%282x%29+=+0

sin%282x%29%282cos%282x%29%5E%22%22+-+sqrt%283%29%29+=+0

sin%282x%29=0      2cos%282x%29%5E%22%22+-+sqrt%283%29+=+0
2x = 0,π,2π,3π       2cos%282x%29=sqrt%283%29
 x = 0,π/2,π,3π/2    cos%282x%29=sqrt%283%29%2F2
                     2x = π/6,11π/6,7π/6,23π/6  
                      x = π/12,11π/12,7π/12,23π/12
8 solutions.

Edwin

Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.

Your starting equation is


    sin(4x) − sqrt(3)*sin(2x) = 0


Substitute (replace) here     sin(4x) = 2sin(2x(*cos(2x).


    2sin(2x)*cos(2x) - sqrt(3)*sin(2x) = 0.


Factor left side


    2sin(2x)*(cos(2x)-sqrt(3)) = 0.


This equation deploys in two equations


    a)  sin(2x) = 0.


        It has the roots  2x = 0, pi,  2pi,  3pi  in the interval  [0,4pi)

        that create the roots

        x = 0,  pi%2F2,  pi,  3pi%2F2  in the interval  [0,2pi).



    b)  cos(2x) = sqrt%283%29%2F2.

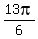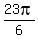        It has the roots  2x = pi%2F6,  11pi%2F6,  13pi%2F6,  23pi%2F6  in the interval  [0,4pi)

        that create the roots

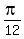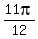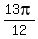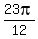        x = pi%2F12,  11pi%2F12,  13pi%2F12,  23pi%2F12  in the interval  [0,2pi).


ANSWER.  There are 8 roots  x = 0,  pi%2F2,  pi,  3pi%2F2

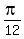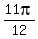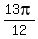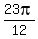                                pi%2F12,  11pi%2F12,  13pi%2F12,  23pi%2F12  in the interval  [0,2pi).

Solved.


/////////////


Find the differences between my solution and the solution by Edwin.