SOLUTION: An infinite increasing list of numbers has the property that the median of the first n terms equals the nth odd positive integer. How many numbers in the list are less than 2018?

Algebra ->  Average -> SOLUTION: An infinite increasing list of numbers has the property that the median of the first n terms equals the nth odd positive integer. How many numbers in the list are less than 2018?      Log On


   

Question 1178119: An infinite increasing list of numbers has the property that the median of the
first n terms equals the nth odd positive integer. How many numbers in the
list are less than 2018?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
An infinite increasing list of numbers has the property that the median of
the first n terms equals the nth odd positive integer. 
Let the first 3 terms be a,b,c, where a < b < c. the median is b.
There are 3 terms, the 3rd odd integer is 5, so b=5.
The sequence so far is a,5,c.  

Let the first 4 terms be a,5,c,d where a < 5 < c < d. the median is (5+c)/2.
There are 4 terms, the 4th odd integer is 7, so 
(5+c)/2=7
    5+c=14
      c=9
The sequence so far is a,5,9,d.

Let the first 5 terms be a,5,9,d,e where a < b < c < d < e. the median is 9.
There are 5 terms, the 5th odd integer is 9.
The sequence so far is a,5,9,d,e.

Let the first 6 terms be a,5,9,d,e,f where a < b < c < d < e < f. the median
is (9+d)/2. There are 6 terms, the 6th odd integer is 11.
(9+d)/2=11
    9+d=22
      d=13
The sequence so far is a,5,9,13,e,f.

We guess from the middle 3 terms that the sequence is the arithmetic
sequence 1,5,9,13,17,21,...

If so, the nth term is

a%5Bn%5D=a%5B1%5D%2B%28n-1%29D, where a1 = 1, D = 4

a%5Bn%5D=1%2B%28n-1%294

So we set 

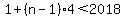
a%5Bn%5D=1%2B%28n-1%294%3C2018
1%2B%28n-1%294%3C2018
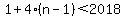
1%2B4%28n-1%29%3C2018
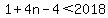
1%2B4n-4%3C2018
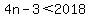
4n-3%3C2018
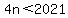
4n%3C2021
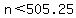
n%3C505.25
n%3C=505


So there are 505 numbers in the list less than 2018.

Edwin