Question 1177975: Find an equation of the parabola of the form y=ax^2+bx+c that passes through the following three points.
(1,2),(-1,6),(3,6)
Found 3 solutions by mananth, MathLover1, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! let the equation of the parabola be y=ax2+bx+c.
the parabola passes through the point plug plug (1,2), then 2=a+b+c.
the parabola passes through the point (−1,6), then 6=a−b+c.
the parabola passes through the point plug (3,6), then 6=9a+3b+c.
Thus, we have obtained the following system with three variables
⎧⎩⎨a+b+c=2
a−b+c=69
a+3b+c=6
Solving the system of linear equations , we get that a=1, b=−2, c=3.
Therefore the equation of the parabola is y=x2−2x+3.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
( , , ),( ),( , , ),( ),( , , ) )
 ...........use ( ...........use ( , , ) )

 .....solve for .....solve for 
 .............eq.1 .............eq.1
 ...........use ( ...........use ( , , ) )

 .....solve for .....solve for 
 .............eq.2 .............eq.2
from eq.1 and eq.2 we have
 ............solve for ............solve for





go to
 ...........use ( ...........use ( , , ) and ) and 
 .........solve for .........solve for 




 ..............eq.3 ..............eq.3
from eq.1 and eq.3 we have
 ....substitute ....substitute 

 ......solve for ......solve for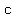


 ......cross multiply ......cross multiply
 ..........simplify, divide by ..........simplify, divide by 


go to
 .............eq.2,substitute .............eq.2,substitute  and and 


so, your equation is


Answer by ikleyn(52799)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is very SPRECIAL among thousands other similar problems,
and THREFORE it can be solved MENTALLY without writing and solving any equations.
Indeed, notice that of the three given points, two points have equal y-coordinate, (-1,6) and (3,6).
It means that these two points are symmetric relative to the vertical symmetry axis of the parabola.
It also means that vertical symmetry axis of this parabola has x-coordinate which is half of x-coordinates of the two points.
So, the equation of the symmetry axis is x = 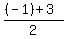 = = 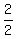 = 1.
After that, you notice that the third point (1,2) has x-coordinate 1, which means that this point (1,2)
lies on the parabola's symmetry axis and, therefore, is the VERTEX of the parabola.
Having this info, we can write the vertex form equation of the parabola
y = a*(x-1)^2 + 2.
To determine the coefficient "a", substitute x= 3 into the equation for the point (3,6). You will get
6 = a*(3-1)^2 + 2
6 - 2 = a*2^2
4 = 4a
a = 1.
Therefore, the parabola equation is
y = (x-1)^2 + 2 (the vertex form), or
y = x^2 - 2x + 1 + 2 = x^2 -2x + 3 (the general form) ANSWER = 1.
After that, you notice that the third point (1,2) has x-coordinate 1, which means that this point (1,2)
lies on the parabola's symmetry axis and, therefore, is the VERTEX of the parabola.
Having this info, we can write the vertex form equation of the parabola
y = a*(x-1)^2 + 2.
To determine the coefficient "a", substitute x= 3 into the equation for the point (3,6). You will get
6 = a*(3-1)^2 + 2
6 - 2 = a*2^2
4 = 4a
a = 1.
Therefore, the parabola equation is
y = (x-1)^2 + 2 (the vertex form), or
y = x^2 - 2x + 1 + 2 = x^2 -2x + 3 (the general form) ANSWER
Solved.
|
|
|