Question 1177950: A manufacturer of downhill and cross-country skis reports that manufacturing time is 3 hours and 7 hours, respectively, per ski and that finishing time is 2 hours for each downhill and 2 hours for each cross-crountry ski. There are only 35 hours per week available for the manufacturing process and 18 hours for the finishing process. The average profit is $62 for downhill ski and $63 for cross-country ski. The manufacturer wants to know how many of each type of ski should be made to maximize the weekly profit.
What are the corner points of the feasible region?
I tried solving and got the equations below, but I can't figure out why my vertices are not coming out right.
3x+7y greater than or equal to sign 35
2x+2y greater than or equal to sign 18
I used (0,0) as test points for both and got (0,5) and (11.6,0) for one and (0,9) and (9,0) for the other. my vertices for the feasible region came out to (11.6, 0), (7,2), and (0,9). The (7,2) had a value of 560 when I typed it into my objective function of 62x+63y=z. Any help you can provide would be greatly appreciated.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52805)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let X be the number of downhill skis, and
let Y be the number of cross-country skis.
Then the manufacturing time to produce X downhill skis and Y cross-country skis is 3X + 7Y hours.
and the finishing time to produce X downhill skis and Y cross-country skis is 2X + 2Y hours.
Therefore, the two major constraints are
3X + 7Y <= 35 hours (manufacturing time) (1)
2X + 2Y <= 18 hours (finishing time) (2)
Add to it the standard non-negativity constraints
X >= 0, Y >= 0. (3)
Now we have everything to construct the feasibility region.
For it, you draw the lines 3X + 7Y = 35 and 2X + 2Y = 18 from the constraints.
They are shown in the figure below.
 Plot y =
Plot y = 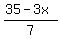 (red) and y = (red) and y = 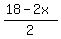 (green)
Inequalities (3) define the first quadrant QI.
The solution set to the given inequalities (the feasibility domain) are the points of the coordinate plane,
that are in QI and belong the quadrilateral below (or on) the red line and below (or on) the green line.
Again: the feasibility domain is the quadrilateral in QI restricted by the red and by the green lines,
adjacent to coordinate axes, including its sides and vertices.
The corner points are
1) P1 = (0,0) the origin of the coordinate plane
2) P2 = (0,5) Y-intercept of the red line
3) P3 = (7,2) intersection of the red line and the green line
4) P4 = (9,0) X-intercept of the green line
At this point, I completed my explanations regarding the corner points.
Next, to solve this minimax problem, compare the values of the objective function z = 62X + 63Y at the corner points.
P1: z = 62*0 + 63*0 = 0
P2: z = 62*0 + 63*5 = 315
P3: z = 62*7 + 63*2 = 560
P4: z = 62*9 + 63*0 = 558
You see that the profit is maximum at point P3.
It gives the solution to the problem : X= 7 downhill skis, Y= 2 cross-country skis with the maximum profit of 560 dollars. ANSWER (green)
Inequalities (3) define the first quadrant QI.
The solution set to the given inequalities (the feasibility domain) are the points of the coordinate plane,
that are in QI and belong the quadrilateral below (or on) the red line and below (or on) the green line.
Again: the feasibility domain is the quadrilateral in QI restricted by the red and by the green lines,
adjacent to coordinate axes, including its sides and vertices.
The corner points are
1) P1 = (0,0) the origin of the coordinate plane
2) P2 = (0,5) Y-intercept of the red line
3) P3 = (7,2) intersection of the red line and the green line
4) P4 = (9,0) X-intercept of the green line
At this point, I completed my explanations regarding the corner points.
Next, to solve this minimax problem, compare the values of the objective function z = 62X + 63Y at the corner points.
P1: z = 62*0 + 63*0 = 0
P2: z = 62*0 + 63*5 = 315
P3: z = 62*7 + 63*2 = 560
P4: z = 62*9 + 63*0 = 558
You see that the profit is maximum at point P3.
It gives the solution to the problem : X= 7 downhill skis, Y= 2 cross-country skis with the maximum profit of 560 dollars. ANSWER
Solved.
///////////
To see many other similar solved problems, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
Learn the subject from there.
|
|
|