SOLUTION: Determine the exact value(s) of k such that (k+2)x^2 −6 = kx −1 has one solution. I need help asap thank you!!!!

Algebra ->  Graphs -> SOLUTION: Determine the exact value(s) of k such that (k+2)x^2 −6 = kx −1 has one solution. I need help asap thank you!!!!      Log On


   

Question 1177949: Determine the exact value(s) of k such that (k+2)x^2 −6 = kx −1 has one solution.
I need help asap thank you!!!!
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Determine the exact value(s) of+k such that+%28k%2B2%29x%5E2+-6+=+kx+-1 has one solution.
%28k%2B2%29x%5E2+-6+-+kx+%2B1=0
%28k%2B2%29x%5E2-+kx++-5+=0
=> a=%28k%2B2%29, b=-k,+c=-5
use discriminant:
If discriminant,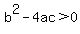+b%5E2+-+4ac+%3E+0, two solutions exist.
If discriminant, b%5E2+-+4ac+=+0, one solution exists.
If discriminant, 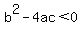b%5E2+-+4ac+%3C+0, no solution exists
so, you need:
b%5E2-4ac=0+....substitute a,b, and c
%28-k%29%5E2-4%28k%2B2%29%28-5%29=0+
k%5E2%2B20k%2B40=0 .........using quadratic formula, we get
k+=+2+%28sqrt%2815%29+-+5%29
k+=+-2+%285+%2B+sqrt%2815%29%29

+%282%28sqrt%2815%29+-+5%29%2B2%29x%5E2+-6+=+2+%28sqrt%2815%29+-+5%29x+-1
%282sqrt%2815%29+-+8%29x%5E2+-+6=2+%28sqrt%2815%29+-+5%29x+-1 -> has one solution
or
+%28-2%28sqrt%2815%29+%2B5%29%2B2%29x%5E2+-6+=-2%28sqrt%2815%29+%2B+5%29x+-1
-%282sqrt%2815%29%2B8%29x%5E2+-+6=-2%28sqrt%2815%29+%2B+5%29x+-1-> has one solution