Question 1177854: f(x)= x-5 (divied by) 4-x^2
x - intercept(s):
y - intercept:
Vertical Asymptote(s):
Horizontal Asymptote(s):
Domain:
End-Behavior:
Intervals of Increasing/Decreasing:
Intervals of Positive/Negative:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

x - intercept(s):
set 
 ..........since denominator cannot be zero, use numerator only ..........since denominator cannot be zero, use numerator only
 => =>
x - intercept is at ( , , ) )
y - intercept:
set 


y - intercept is at ( , , ) )
Vertical Asymptote(s):
 .......set denominator equal to zero .......set denominator equal to zero
 => => => => and and 
Horizontal Asymptote(s):

Degree of numerator is less than degree of denominator: horizontal asymptote at  . .
Domain:
{  element element  : : 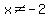 and and  } }
or

range:


Rewrite the above equation for x in standard form and solve using quadratic formulae



 -> a=y, b=1, c=-(4y+5) -> a=y, b=1, c=-(4y+5)
Find the discriminant to the above equation

.............=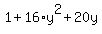
.............=
Using the quadratic formulas, the above equation gives the solutions

The solutions  are real if are real if  and and  ≠ ≠ . .
Hence we need to solve the inequality
 and solution will be and solution will be


End-Behavior:
function end-behavior of 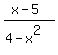 : :
as  , , 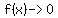 , and , and
as  , ,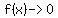
Intervals of Increasing/Decreasing:
If  ' ' 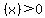 then then 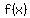 is increasing is increasing
If  ' ' 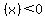 then then 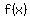 is decreasing is decreasing
 ...derivate ...derivate
 ' '
Increasing 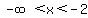 , and , and 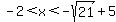 , ,
Decreasing:
Intervals of Positive/Negative:
positive when 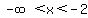 U U 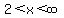
negative when 

|
|
|