SOLUTION: The legs of a right triangle are in the ratio 1:2. The angle bisector to the short leg divides it into two segments, one of which is 1cm longer than the other. Express the perim

That means the right triangle is similar to this right triangle

We draw the angle bisector (in green), and let the two segments be 
x and x+1:



A famous theorem says:

The bisector of an angle of a triangle divides the opposite side into
segments that are proportional to the adjacent sides.

We also know the ratio is 2:√5 from the similar right triangle at the top.



Solve for x and get



So the right side of the triangle is  = 

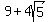Since the side corresponding to 1 is 9+4√5, we know the scale factor is
9+4√5.

Since this triangle (the one at the top)



has perimeter 3+√5, we just multiply that by the scale factor:



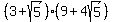and get 

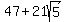   <--answer

Edwin