|
Question 1177760: Find an equation of the set of points on a plane such that the sum of the distances between each point of the set and the points (0,3) and (0,-3) is 10 units.
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find an equation of the set of points on a plane such that the sum of the distances
between each point of the set and the points (0,3) and (0,-3) is 10 units.
~~~~~~~~~~~~~
This set of points is the ellipse on a coordinate plane, centered at the origin
and having focuses at given points (0,3) and (0,-3).
Its major axis is vertical; minor axis is horizontal;
the major semi-axis "a" has the length
(a-3) + (a-(-3)) =10, or, equivalently, (a-3) + (a+3) = 10, 2a = 10, a = 5 units.
The minor semi-axis "b" has the length b = 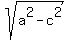 = =  = = 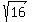 = 4 units.
The canonical equation of this ellipse is = 4 units.
The canonical equation of this ellipse is
 + + 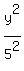 = 1. ANSWER = 1. ANSWER
Solved.
-------------------
On canonical equation for ellipses, see the lesson
- Ellipse definition, canonical equation, characteristic points and elements
in this site.
|
|
|
| |