SOLUTION: (2, 3𝜋/4) Find three additional polar representations of the point, using −2𝜋 < 𝜃 < 2𝜋. (r, 𝜃) = (r, 𝜃) = (r, 𝜃) =

Algebra ->  Trigonometry-basics -> SOLUTION: (2, 3𝜋/4) Find three additional polar representations of the point, using −2𝜋 < 𝜃 < 2𝜋. (r, 𝜃) = (r, 𝜃) = (r, 𝜃) =       Log On


   

Question 1177709: (2, 3𝜋/4)
Find three additional polar representations of the point, using −2𝜋 < 𝜃 < 2𝜋.
(r, 𝜃) =
(r, 𝜃) =
(r, 𝜃) =

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
(2, 3pi%2F4)
Find three additional polar representations of the point, using 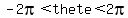-2pi+%3C+thete+%3C+2pi.
(r, theta) =(r, %28theta+%2B-+2n%2Api%29)
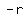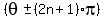(r, theta) =(-r, %28theta+%2B-+%282n%2B1%29pi%29)
put n=1
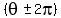(r, %28theta+%2B-+2pi%29)
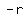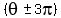(-r,%28theta+%2B-+3pi%29)

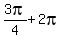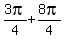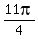(r, theta) =(2, 3pi%2F4%2B2pi)=(2, 3pi%2F4%2B8pi%2F4)=(2, 11pi%2F4)
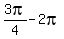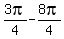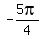(r, theta) =(2, 3pi%2F4-2pi)=(2, 3pi%2F4-8pi%2F4)=(2, -5pi%2F4)
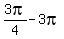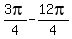(r, theta) =(-2, 3pi%2F4-3pi)=(2, 3pi%2F4-12pi%2F4)=(-2, -9pi%2F4)