Question 1177707: steven just deposited $10,000 in a bank account that has a 12 percent nominal interest rate, and the interest is compounded monthly. steven also plans to contribute another $10,000 to the account one year (12 months) from now and another $20,000 to the account two years from now. how much will be in the account three years (36 months) from now?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the nominal interest rate is 12% per year.
the effective interest rate is 1% per month.
this yields an effective interest rate of ((1.01)^12 -1) * 100 = 12.68250301% per year.
your growth factor per year is (1.01)^12 = 1.1268250301.
you start with 10,000
one year later, the value is equal to 10,000 * 1.1268250301 = 11,268.21503.
you add 10,000 to that to get 21,268.21503.
one year later, the value of that is equal to 21,268.21503 * 1.1268250301 = 23,965.59679.
you add 10,000 to that to get 33,965.59679.
one year later, the value of that is equal to 33,965.59679 * 1.1268250301 = 38,273.28462.
you could also have used a financial calculator to get the same results.
one such calculator can be found at https://arachnoid.com/finance/index.html
the inputs to this calculator are shown below.
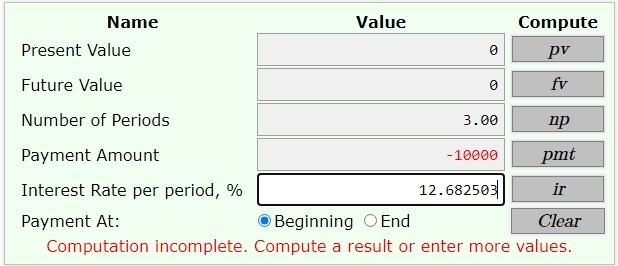
the output from this calculator is shown below.
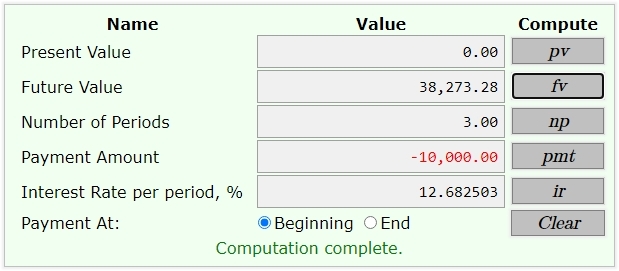
since you are dealing in years, then the effective interest rate per year had to be used.
that was calculated as follows:
the nominal interest rate per year is 12%.
the effective monthly interest rate per year is 1%.
the effective interest rate per year is (1.01)^12 = 1.12682503 -1 = .12682503 * 100 = 12.682503%.
ir equal to 12.682503 was entered as input to the problem as shown in the first display.
note that yearly payments were made at the beginning of each year.
|
|
|