Question 117765This question is from textbook
: A plane traveled 864 miles to Kampala and back. The trip there was with the wind. It took 9 hours. The trip back was into the wind. The trip back took 16 hours. Find the speed of the plane in still air and the speed of the wind. show work.
This question is from textbook
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! A plane traveled 864 miles to Kampala and back. The trip there was with the wind. It took 9 hours. The trip back was into the wind. The trip back took 16 hours. Find the speed of the plane in still air and the speed of the wind. show work.
-----------------
Let plane speed be "p"; Let wind speed be "w".
------------------
To Kampala DATA:
Distance = 864 miles ; Time = 9 hrs. Rate = 864/9 = 96 mph
-----------------
From Kampala DATA:
Distance = 864 miles ; time = 16 hrs ; Rate = 864/(16) = 54 mph
-------------------
EQUATIONS:
p+w = 96
p-w = 54
-----------
2p = 150
p = 75 mph (speed of the plane in still air)
----------
75+w = 96
w = 21 mph (speed of the wind)
============
Cheers,
Stan H.
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! This is a distance - rate - time problem. The formula is  .
Let's say that the speed of the plane in still air is 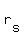 and the speed of the wind is  . So when the plane is travelling with the wind, its speed relative to the ground is 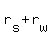 , and when travelling against the wind,  .
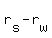So the description of the trip to Kampala is  , and the description of the return trip is 
Start by dividing the 'To' equation by 9:  , and
dividing the 'From' equation by 16: 
This gives us two linear equations in two unknowns. Since the coefficient on is 1 in the first equation and -1 in the second equation, it is a simple matter to eliminate this variable by adding the two equations term by term to get:
Now that we know the speed in still air is 75 mph, we can see that the wind speed must have been  , 21 mph.
***********************************
Note: The problem as stated has a slight ambiguity to the wording. It is not absolutely clear that the one-way distance from the starting point to Kampala is 864 miles. The way it is worded, it could have meant that the round trip distance was 864 miles. However, once I solved the problem using the first meaning and discovered the result was 75 mph airspeed, I realized that the first interpretation had to be the correct one. The other 864 mile round trip interpretation would have yielded an airspeed of half of 75, or 37.5 mph. 75 mph is pretty darn slow for an airplane, but 37.5 mph is downright absurd. I'm sharing this analysis because I want you to always consider the reasonability of your answers when you work these types of problems.
Hope that helps,
John
Super Double-Plus Extra Credit: This problem uses miles and miles per hour as units, and one presumes that to mean statute miles, or ground miles. Since airspeed and wind speed are generally expressed in knots (nautical miles per hour), what would 75 mph and 21 mph be if the unit were knots? Hint: 1 statute mile = 1760 yards. 1 nautical mile = 2000 yards. There must be a proportion here somewhere.
|
|
|
