SOLUTION: The positive numbers p and q are the 2nd and 14th terms respectively of an arithmetic progression where the first term is 1. Given also that p, 9 and q are 3 successive terms of a

From the first statement, we have


    p = 1 + d,       (1)

    q - p = 12d      (2)


From the second statement, we have


    p*q = 81.        (3)


Thus we have three equations for three unknowns  p, q an d, so the problem is solvable.


We reduce three equations (1), (2) and (3) to one equation


    (1+d)*(1+13d) = 81.


It is a quadratic equation, and it can be solved formally.


It has two roots  d= 2  and  d= .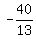


Only the root d= 2 produces positive p and q.


So, the solution to the problem are the values  d= 2. p = 1+d = 3  and  q= 27.