SOLUTION: Bob claims he can roll triples with three dice in fewer than 10 rolls. a) What is the expected number of rolls that it would take to roll the first set of triples? b) What is

We figure the probability that he will roll triples in 1 roll.

We imagine that one die is red, one die is blue, and one die is yellow.

The probability that the red die lands on one of the 6 possible numbers is 6
ways out of 6, or 6/6 or 1. {He's certain to get something!)

Then Bob's probability that the blue die lands on the same number that the red
one landed on is 1 way out of 6, or 1/6.

Then his probability that the yellow die lands on one the same number that
the red and blue dice landed on is also 1 way out of 6, or 1/6.

So the probability of rolling triples on a single throw of three dice is
(1)(1/6)(1/6) or 1/36.

The probability of not rolling a triple on a single throw of three dice is
 or .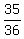

The probability of rolling a triple on the first roll is .

So the expectation of rolling a triple on the first try is .

The probability of not rolling a triple on the 1st roll but rolling a
triple on the 2nd roll is 

So the expectation of not rolling a triple until the 2nd try is 

The probability of not rolling a triple on the 1st or 2nd roll but 
rolling a triple on the 3rd roll is 

So the expectation of not rolling a triple until the 3rd try is 

The probability of not rolling a triple on the 1st, 2nd, or 3rd roll
but rolling a triple on the 4th roll is 

So the expectation of not rolling a triple until the 4th try is 

We can generalize.

The expectation of not rolling a triple until the Nth try is 

Theoretically, Bob could spend his whole life rolling the three dice without
ever rolling a triple.  So the expected number of rolls it would take him to
roll a triple is the sum of an infinite series.



Multiply and divide by 35



We can factor out 



The summation is a arithmetico-geometric series. The sum is given by
Gabriel's Staircase Formula, which is  

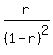 for 0 < r < 1

We will find the summation first, then we will multiply by 1/35.

Here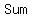 



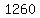Now we must multiply that by 1/35, as we said above, so the answer to a)
is 

So if every day for a year, Bob rolled the three dice until he got a triple,
he would find that on the average it takes him about 36 rolls.  Once in a
while, he'll get a triple the first time, and other times it will take him
100 or more rolls to get a triple.  But on the average, it'll take him about
36 rolls.

Answer to a) is 36

The probability of rolling a triple on the first roll is 

The probability of not rolling a triple on the 1st roll but rolling a
triple on the 2nd roll is 

The probability of not rolling a triple on the 1st or 2nd roll but 
rolling a triple on the 3rd roll is 

The probability of not rolling a triple on the 1st, 2nd, or 3rd roll but 
rolling a triple on the 4th roll is 

The sum of those probabilities is



That's a probability of about 0.10656662 or about 0.1.

 is the answer to b).

So if every day for a year he rolls 3 dice until he gets a triple, about a
tenth of the time it'll take him fewer than 5 rolls to get a triple.

Edwin