Question 1177390: 2x^3+9x^2-4x-18;2x+9 find all zeros
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52868)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution presented by @MathLover1 is INCORRECT and may confuse you.
I came to bring a correct solution.
You consider this rational function
f(x) = 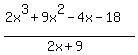 .
Notice that the domain where the function is defined, is the set of all real numbers excluding x = .
Notice that the domain where the function is defined, is the set of all real numbers excluding x = 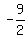 .
Next, factor the numerator .
Next, factor the numerator
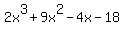 = = 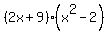 .
Now, considering the given rational function f(x), you can cancel the factor (2x+9) everywhere except of x= .
Now, considering the given rational function f(x), you can cancel the factor (2x+9) everywhere except of x= 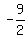 .
It means that the given rational function f(x) is equal to .
It means that the given rational function f(x) is equal to 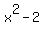 everywhere, except x= everywhere, except x= 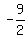 .
Now, the zeroes of the function f(x) are the zeroes of this quadratic binomial .
Now, the zeroes of the function f(x) are the zeroes of this quadratic binomial  =0,
i.e. x= +/- =0,
i.e. x= +/-  .
ANSWER. The given function f(x) has two zeroes in its domain. They are the values x= .
ANSWER. The given function f(x) has two zeroes in its domain. They are the values x=  and x= - and x= -  . .
Solved, answered and explained. // And completed.
///////////
For your better understanding, the function f(x) has a "hole" at the point x= -  . .
This rational function IS NOT DEFINED at this point, although it has the limits at this point from the left side
and from the right side, and these limits are equal.
NETHERTHELESS, the function f(x) IS NOT DEFINED at x= -  : this point is the "hole" point for the function. : this point is the "hole" point for the function.
You should clearly understand it, and the entire problem is designed and intended to teach you to it (!)
Happy learning (!)
|
|
|