|
Question 1177337: When a plane flies with the wind, it can travel 920 miles in 2 hours. When the plane flies in the opposite direction, against the wind, it takes 4 hours to fly the same distance. Find the rate of the plane in still air and the rate of the wind.
Found 4 solutions by mananth, ikleyn, josgarithmetic, n2:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website!
let the rate of the plane in still air be x
and the rate of the wind be y
rate with wind =( x+y) mph
distance = 920 miles
time = 2 hours
d/r = t
920/(x+y) =2
2x+2y =920
/2
x+y = 460 --------------(1)
Against wind rate = (x-y)
920/(x-y) = 4
4x-4y = 920
/4
x-y = 230------------------(2)
Add equation (1) & (2)
2x = 690
x= 345
the rate of the plane in still air 345 mph
the rate of the wind be 115 mph
Answer by ikleyn(53646)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When a plane flies with the wind, it can travel 920 miles in 2 hours.
When the plane flies in the opposite direction, against the wind, it takes 4 hours to fly the same distance.
Find the rate of the plane in still air and the rate of the wind.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the rate of the plane at no wind (in miles per hour)
and v be the rate of the wind (in the same units).
Then the effective rate of the plane with the wind is u + v
and the effective rate of the plane against the wind is u - v.
From the problem, the effective rate of the plane with the wind is the distance of 920 miles
divided by the time of 2 hours 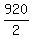 = 460 mph.
The effective rate of the plane against the wind is the distance of 920 miles
divided by the time of 4 hours = 460 mph.
The effective rate of the plane against the wind is the distance of 920 miles
divided by the time of 4 hours 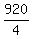 = 230 mph.
So, we have two equations to find 'u' and 'v'
u + v = 460, (1)
u - v = 230. (2)
To solve, add equations (1) and (2). The terms 'v' and '-v' will cancel each other, and you will get
2u = 460 + 230 = 690 ---> u = 690/2 = 345.
Now from equation (1)
v = 460 - u = 460 - 345 = 115.
ANSWER. The rate of the plane in still air is 345 mph. The rate of the wind is 115 mph km/h. = 230 mph.
So, we have two equations to find 'u' and 'v'
u + v = 460, (1)
u - v = 230. (2)
To solve, add equations (1) and (2). The terms 'v' and '-v' will cancel each other, and you will get
2u = 460 + 230 = 690 ---> u = 690/2 = 345.
Now from equation (1)
v = 460 - u = 460 - 345 = 115.
ANSWER. The rate of the plane in still air is 345 mph. The rate of the wind is 115 mph km/h.
Solved.
-------------------------------
This solution produces the same answer as in the post by @mananth, but has an advantage
that it does not contain excessive calculations that the solution by @mananth has.
We, the tutors, write here our solutions not only to get certain numerical answer.
We write to teach - and, in particular, to teach solving in a right style.
This style solving presented in my post, is straightforward with no logical loops.
The solution presented in the post by @mananth has two logical loops.
One loop in the @mananth post is writing
d/r = t ---> 920/(x+y) = 2 ---> 2x + 2y = 920 ---> /2 ---> x+y = 460,
while in my solution I simply write for the effective rate
u + v = 920/2 = 460.
Second loop in the @mananth post is writing
920/(x-y) = 4 ---> 4x - 4y = 920 ---> /4 ---> x-y = 230,
while in my solution I simply write for the effective rate upstream
u - v = 920/4 = 230.
It is why I presented my solution here and why I think it is better than the solution by @mananth:
- because it teaches students to present their arguments in a straightforward way, without logical zigzags.
@mananth repeats his construction of solution with no change for all similar problems on flies
with and against the wind simply because his COMPUTER CODE is written this way.
But this way is not pedagogically optimal - in opposite, it is pedagogically imperfect.
Answer by josgarithmetic(39749)   (Show Source): (Show Source):
You can put this solution on YOUR website!
s, speed if no wind
w, speed of the wind
SPEED TIME DISTANCE
WITH WIND s+w 2 920
AGAINST WIND s-w 4 920
Distance Divided By Time is speed.


.
.
Answer by n2(66)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A kayak can travel 24 miles downstream in 2 hours, while it would take 12 hours to make the same trip upstream.
Find the speed of the kayak in still water, as well as the speed of the current.
Let k represent the speed of the kayak in still water, and let c represent the speed of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let k be the rate of the kayak in still water (in miles per hour)
and c be the rate of the current (in the same units).
Then the effective rate of the kayak downstream is k + c
and the effective rate of the kayak upstream is k - c.
From the problem, the effective rate of the kayak downstream is the distance of 24 miles
divided by the time of 2 hours  = 12 mph.
The effective rate of the plane upstream is the distance of 24 miles
divided by the time of 12 hours = 12 mph.
The effective rate of the plane upstream is the distance of 24 miles
divided by the time of 12 hours 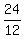 = 2 mph.
So, we have two equations to find 'k' and 'c'
k + c = 12, (1)
k - c = 2. (2)
To solve, add equations (1) and (2). The terms 'c' and '-c' will cancel each other, and you will get
2k = 12 + 2 = 14 ---> k = 14/2 = 7.
Now from equation (1)
v = 12 - u = 12 - 7 = 5.
ANSWER. The rate of the kayak in still water is 7 mph. The rate of the current is 5 mph km/h. = 2 mph.
So, we have two equations to find 'k' and 'c'
k + c = 12, (1)
k - c = 2. (2)
To solve, add equations (1) and (2). The terms 'c' and '-c' will cancel each other, and you will get
2k = 12 + 2 = 14 ---> k = 14/2 = 7.
Now from equation (1)
v = 12 - u = 12 - 7 = 5.
ANSWER. The rate of the kayak in still water is 7 mph. The rate of the current is 5 mph km/h.
Solved.
|
|
|
| |