SOLUTION: For what values of k' the following system has 2x+y=0 x+ 2y + kz = -1 x +k²z = 1 (a) Unique Solution (b) No solution.

2x + y + 0z = 0

x + 2y + kz = -1

x + 0y + z = 1



Notice that y can be eliminated...



Using the first equation, y=-2x, then substituting this into the 2nd eqn gives:



x + 2(-2x) + kz = -1

-3x + kz = -1       (1)



and eqn (2) is just the 3rd eqn without the 0y:

x + z = 1        (2)





 = 



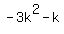
Unique solution will be when 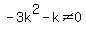   or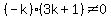 

[Edited line above to have 2nd factor of 3k+1, it was a typo, the math below 

was correct.]



so when 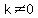 and 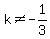 there is a unique solution.



Spot check one unique solution, let k=1, then eqns(1) and (2) give:



-3x + z = -1

 x + z  = 1 

------------

 -4x = -2   --> x=1/2 --> z=1/2  (using the bottom eqn)



Check using top eqn:  -3(1/2) + (1/2) = -3/2 + 1/2 = -1 (ok)

--------------

--------------







When k=0 or k=-1/3, the determinant is zero and there is either no solution or an infinite number of solutions (you can use Gaussian elimination to figure out which situation applies for these two cases, or you can plug in k=0 into eqns (1) & (2) and try to solve, then repeat for k=-1/3).



I think there is no solution for either value of k (you should get two inconsistent equations in x and z for each value of k)...