Question 1177105: given sequence 2;5;8
2.1.1 if the pattern continues
, then write down the next two terms
2.2.2 prove that none of the terms of this sequence are perfect squares
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given sequence  ; ; ; ;
2.1.1 if the pattern continues, then write down the next two terms
as you can see, common difference is  , so next two terms are , so next two terms are  and and 
2.2.2 prove that none of the terms of this sequence are perfect squares
Let each term of the given arithmetic progression be defined as
 , where , where  and and 


Hence, each term of the AP is of the form 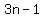 , , ∈ ∈  . .
We know that any integer is of the form 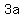 , ,  or or  for for  ∈ ∈ . .
Taking  , we have , we have  , with , with  . .
Taking  , we have , we have  , where , where 
Taking  , we have , we have  , with , with 
Hence, we can see that a perfect square is always of the form  or or 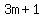 , where , where  is an integer. is an integer.
Hence, we can infer that a perfect square is not of the form  . .
Also, we have each term of the given AP to be of the form  . .
Hence,  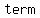 of the given AP is a of the given AP is a  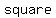 . .
|
|
|