Question 1176904: If a player rolls two dice and gets a sum of 11, he wins $ 20. if he gets a sum of 7 he wins $ 5. The cost to play the game is $ 3. Find the expectation of the game ?
I built a probability distribution based on gain and calculated the mean. I get an answer of $-0.39, but the key shows a different answer. Can you show me what I am doing incorrectly?
Answer by ikleyn(52864)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When rolling two dice, in all, 36 equally likely outcomes are possible.
Of them, there are 2 outcomes that produce the sum of 11 : (5,6) and (6,5).
Also, there are 6 outcomes that produce the sum of 7: (1,6), (2,5), (3,4), (4,3), (5,2) and (6,1).
So, you can win $20 with the probability  and
you can win $5 with the probability and
you can win $5 with the probability  .
So, your winning expectation is .
So, your winning expectation is 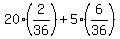 = = 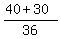 = = 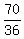 = 1.94 dollars.
From it, you should subtract the cost of the play of $3, so the expectation of the game is $1.94 - $3.00 = - $1.06.
In other words, you will lose 1.06 dollars statistically at each game, in average. = 1.94 dollars.
From it, you should subtract the cost of the play of $3, so the expectation of the game is $1.94 - $3.00 = - $1.06.
In other words, you will lose 1.06 dollars statistically at each game, in average.
Solved.
-------------
See the lessons
- Rolling a pair of fair dice
- Math expectation of winning in games with rolling pair of dice
in this site.
You will find many similar solved problems there.
|
|
|