|
Question 1176882: At an annual board meeting company X is deciding whether or not to take the company public. Each board member can vote “yes”, “no”, or “abstain.” If there are n-board members, then how many different ways can the votes be cast? Express your answer as a recursive function, f(n). Do not forget to include any necessary base case(s).
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's craft a recursive function to model this scenario.
**Recursive Function**
Let `f(n)` represent the number of different ways the votes can be cast with `n` board members.
**Base Case**
* `f(1) = 3`
If there's only one board member, they have three choices: "yes", "no", or "abstain".
**Recursive Step**
For `n > 1` board members:
* Consider the first board member. They have 3 options.
* For each of those options, the remaining `n-1` members can vote in `f(n-1)` ways.
Therefore, the recursive relation is:
* `f(n) = 3 * f(n-1)`
**Complete Recursive Function**
```
f(n) = {
3, if n = 1
3 * f(n-1), if n > 1
}
```
**Explanation**
This function captures the essence of the voting process. Each member adds a factor of 3 (their voting choices) to the total number of possible outcomes. The recursion breaks down the problem by considering one member at a time.
**Example**
Let's calculate the number of ways for a small board with 3 members:
* `f(1) = 3`
* `f(2) = 3 * f(1) = 3 * 3 = 9`
* `f(3) = 3 * f(2) = 3 * 9 = 27`
So, with 3 board members, there are 27 different ways the votes can be cast.
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At an annual board meeting company X is deciding whether or not to take the company public.
Each board member can vote “yes”, “no”, or “abstain.” If there are n-board members,
then how many different ways can the votes be cast? Express your answer as a recursive function, f(n).
Do not forget to include any necessary base case(s).
~~~~~~~~~~~~~~~~~~~~~~~
It is much easier to get / (to write) the final formula, than the recursive formula.
For n members in the board, the full set of possible answers has 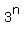 elements. elements.
It is OBVIOUS, since there are 3 possible answers foe each member, and these answers are independent for members.
So, the request to write a recursive function is unnecessary complication of the problem.
|
|
|
| |