SOLUTION: Graph the polynomial function that has the following properties: Negative leading coefficient with an odd degree Zeros at x = -3 with multiplicity 4, x = 0 with multiplicity 1,

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Graph the polynomial function that has the following properties: Negative leading coefficient with an odd degree Zeros at x = -3 with multiplicity 4, x = 0 with multiplicity 1,      Log On


   

Question 1176819: Graph the polynomial function that has the following properties:
Negative leading coefficient with an odd degree
Zeros at x = -3 with multiplicity 4, x = 0 with multiplicity 1, and x = 3 with multiplicity 2

Homework question from Hans Beauvoir
Found 3 solutions by greenestamps, MathLover1, Edwin McCravy:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Moving let to right....

odd degree with negative leading coefficient: the graph goes to +infinity for large negative values.

root of multiplicity 4 at x = -3: the graph touches the x-axis at x = -3 but stays positive; and it is very flat near there.

root of multiplicity 1 at x = 0: the graph crosses the x-axis (from positive to negative) at x=0.

root of multiplicity 2 at x = 3: the graph just touches the x-axis at x = 3 and stays negative.

odd degree with negative leading coefficient: the graph goes to -infinity for large positive values.

Put it all together....

graph%281200%2C400%2C-5%2C5%2C-50%2C50%2C-%28%28x%2B3%29%5E4%29%28x%29%28x-3%29%5E2%29

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Negative leading coefficient with an odd degree:

Zeros at x+=+-3 with multiplicity 4,
x-%28-3%29=x%2B3=> you have 4 times factor %28x%2B3%29 or %28x%2B3%29%5E4
x+=+0 with multiplicity 1,
x-0=x=> you have 1 time factor x
x+=+3 with multiplicity 2
x-3=> you have 2 times factor %28x-3%29, or %28x-3%29%5E2
then your polinomial is equal to product of the factors above multiplied by -1 because negative leading coefficient :
f%28x%29=-%28%28x%2B3%29%5E4%2Ax%2A%28x-3%29%5E2%29
f%28x%29=-x%5E7+-+6x%5E6+%2B+9x%5E5+%2B+108x%5E4+%2B+81x%5E3+-+486x%5E2+-+729x

download-1



Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!


Negative leading coefficient with an odd degree
Zeros at x = -3 with multiplicity 4, x = 0 with multiplicity 1, and x = 3 with multiplicity 2
We'll look at the zero properties first

Zero at
x = -3 with multiplicity 4

That means (x+3)4 is a factor of the polynomial. 4 is even
so it will "bounce" off the x axis at x=-3.
x = 0 with multiplicity 1,
 
That means (x-0)1 or just x is a factor of the polynomial. 1 is
odd so it will cut through the x axis at x=0.
x = 3 with multiplicity 2
That means (x-3)2 is a factor of the polynomial. 2 is even
so it will "bounce" off the x axis at x=3.

So we put those three factors together

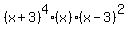%28x%2B3%29%5E4%28x%29%28x-3%29%5E2

The greatest power of x that will occur is x7
Negative leading coefficient with an odd degree
That has an odd degree, 7, but not a negative leading coefficient.
So we must multiply a negative sign in front:

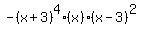-%28x%2B3%29%5E4%28x%29%28x-3%29%5E2

It has a negative leading coefficient so it will go down on the extreme
right.  It has odd degree so it will do the opposite, go up, on the extreme
left.

Multiply it out, and label the polynomial function p(x)

p%28x%29=-x%5E7+-+6x%5E6+%2B+9x%5E5+%2B+108x%5E4+%2B+81x%5E3+-+486x%5E2+-+729x



Edwin