|
Question 1176815: A motorboat travels 165 kilometers in 3 hours going upstream. It travels 207 kilometers going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current?
Found 3 solutions by mananth, ikleyn, n2:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! let rate of the boat in still water be x km/h
and the rate of the current be y km/h
Upstream speed = x-y
Time = D/S
165/(x-y) = 3
3x-3y=165 -----------(1)
Downstream speed = x+y
207/(x+y) =3
3x+3y= 207-----------(2)
Add equations (1) & (2)
6x=207+165
6x = 372
x= 62
speed of boat in still water= 62 km/h
Plug x to get y
3x-3y=165
186-3y =165
3y= 21
y=7
Speed of current is 7 km/h
Answer by ikleyn(53614)  (Show Source):
You can put this solution on YOUR website! .
A motorboat travels 165 kilometers in 3 hours going upstream.
It travels 207 kilometers going downstream in the same amount of time.
What is the rate of the boat in still water and what is the rate of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The way how @mananth solves this problem (and many other similar problems) reminds me
of dancing around a bonfire with a tambourine, but not solving a mathematical problem.
It is impossible to teach students, giving them such a template as in the post by @mananth.
Therefore, below I give a normal mathematical solution for this problem..
Let u be the rate of the boat in still water (in kilometers per hour), and
let v be the rate of the current.
Then the effective rate of the boat downstream is (u+v) km/h,
while its effective rate upstream is (u-v) km/h.
From the given data in the problem, we can calculate the effective rate downstream as
u + v = 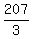 = 69 km/h
and the effective rate upstream as
u - v =  = 55 km/h.
So, we have two equations
u + v = 69, (1)
u - v = 55. (2)
Find 'u' using the elimination method. For it, add equations (1) and (2).
The terms 'v' and '-v' will cancel each other, and you will get
2u = 69 + 55 = 124 ---> u = 124/2 = 62 km/h.
Now from equation (1) find
v = 69 - 62 = 7 km/h.
At this point, the problem is solved completely.
ANSWER. The rate of the boat in still water is 62 km/h, and the rate of the current is 7 km/h.
Solved in full by a standard algebra way with complete explanations.
Ignore the post by @mananth and never ever look in such explanations as in his post.
His post is produced by a computer code, but the code is written in a bad anti-pedagogical way.
Answer by n2(51)  (Show Source):
You can put this solution on YOUR website! .
A motorboat travels 165 kilometers in 3 hours going upstream.
It travels 207 kilometers going downstream in the same amount of time.
What is the rate of the boat in still water and what is the rate of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the rate of the boat in still water (in kilometers per hour), and
let v be the rate of the current.
Then the effective rate of the boat downstream is (u+v) km/h,
while its effective rate upstream is (u-v) km/h.
From the given data in the problem, we can calculate the effective rate downstream as
u + v = 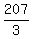= 69 km/h
and the effective rate upstream as
u - v = = 55 km/h.
So, we have two equations
u + v = 69, (1)
u - v = 55. (2)
Find 'u' using the elimination method. For it, add equations (1) and (2).
The terms 'v' and '-v' will cancel each other, and you will get
2u = 69 + 55 = 124 ---> u = 124/2 = 62 km/h.
Now from equation (1) find
v = 69 - 62 = 7 km/h.
At this point, the problem is solved completely.
ANSWER. The rate of the boat in still water is 62 km/h, and the rate of the current is 7 km/h.
Solved in full by a standard algebra way with complete explanations.
|
|
|
| |
