Question 1176777: Solve.
The average value of a certain type of automobile was $14,520 in 1991 and depreciated to $6240 in 1995. Let y be the average value of the automobile in the year x, where x = 0 represents 1991. Write a linear equation that models the value of the automobile in terms of the year x.
Found 2 solutions by ikleyn, ewatrrr:
Answer by ikleyn(52902)   (Show Source):
You can put this solution on YOUR website! .
The average value of a certain type of automobile was $14,520 in 1991 and depreciated to $6240 in 1995.
Let y be the average value of the automobile in the year x, where x = 0 represents 1991.
Write a linear equation that models the value of the automobile in terms of the year x.
~~~~~~~~~~~~~
We use a linear model
y = mx + b
for the depreciated value, starting from x = 0 at 1991.
Therefore, y = m*0 + b = 14520 in 1991, so we just know b= 14520.
To find m, we write
6240 = m*4 + 14520 for the year x= 4 (1995).
From this equation, we find the slope of the linear function
m = 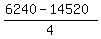 = -2070.
So, the final expression for the depreciated value linear function is
y = -2070*x + 14520, or y = 14520 - 2070x.
Solved and explained.
Answer by ewatrrr(24785)  (Show Source):
|
|
|
