Question 117642: THE SPEED OF AN AIRPLANE IN STILL AIR IS 224KM/H. THE PLANE TRAVELS 733KM AGAINST THE WIND AND 1075KM WITH THE WIND IN A TOTAL TIME OF 15HR. WHAT IS THE SPEED OF THE WIND
Found 3 solutions by solver91311, josmiceli, ankor@dixie-net.com:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please stop using ALL CAPS as it is annoying, hard to read, and is the electronic communication equivalent of SHOUTING. If your excuse is that you cannot type very well, my response is that it is high time you learned -- take a typing course.
***************************************************
Now, to your problem. Let's call the wind speed  . The airplane then travels at . The airplane then travels at 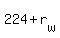 when it is going with the wind, and when it is going with the wind, and 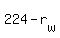 when it is going against the wind. Let's say the time of flight for the 'with the wind' part of the trip is when it is going against the wind. Let's say the time of flight for the 'with the wind' part of the trip is  . That means the time of flight while traveling against the wind must be . That means the time of flight while traveling against the wind must be 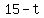 . .
The basic formula that relates distance, rate (speed), and time is  , so let's put it all together: , so let's put it all together:
Eq 1)  , and , and
Eq 2) 
First, solve Eq 2) for  : :

Now we have an expression for  in terms of in terms of  that can be substituted into Eq 1), giving us an equation in a single variable that we can attempt to solve for the value that answers the question, that can be substituted into Eq 1), giving us an equation in a single variable that we can attempt to solve for the value that answers the question,  or wind speed. or wind speed.

First, get everything on one side so that one side is zero. Since we have the variable in both the numerator and denominator, we will end up with a quadratic.

Now we need to distribute 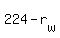

Our lowest common denominator is 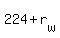 so: so:

Now distribute and collect terms.



So far, we have developed a rational equation. We should now consider whether or not we have any domain problems, i.e. are there values of the variable for which the left side rational expression is undefined? Since we have taken the direction of the wind into account when we made the two expressions for airspeed, we can safely concern ourselves with only positive values for  . Since there are no positive values for . Since there are no positive values for  that would make the denominator zero, we don't need to be concerned about having to exclude a positive root of the equation. Further, we can exclude any negative root(s) of the equation since negative speed is nonsensical in this context. that would make the denominator zero, we don't need to be concerned about having to exclude a positive root of the equation. Further, we can exclude any negative root(s) of the equation since negative speed is nonsensical in this context.
The roots of a rational are simply the root(s) of the numerator polynomial, excluding any values not in the domain of the entire rational expression.
All that is left is to solve:

| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=20975844 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 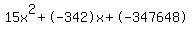 can be factored: can be factored:

Again, the answer is: 164.064643363594, -141.264643363594.
Here's your graph:
 |
Notice that there are two roots given, but we have already concluded that the negative value makes no sense.
Hence, the answer is that the wind speed is 164 km/hr. Although the pluggable quadratic solver that I used gives the answer to several decimal places, it would be incorrect to express the answer with any greater precision than the least precise measurement in the problem givens. Since every bit of given data is presented to the nearest whole number, there shouldn't be any decimal places in the answer.
Point to ponder:
224 km/hr is roughly 140 miles per hour. 164 km/hr is roughly 100 miles per hour. I find it highly improbable that the flight described would ever take place. It would be extraordinarily difficult to find a pilot who was simultaneously smart enough to fly an airplane at all and stupid enough to take his 140 mph top speed aircraft up into the teeth of a 100 mph wind.
Hope this helps,
John
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE SPEED OF AN AIRPLANE IN STILL AIR IS 224KM/H. THE PLANE TRAVELS 733KM AGAINST THE WIND AND 1075KM WITH THE WIND IN A TOTAL TIME OF 15 HR. WHAT IS THE SPEED OF THE WIND
:
Let x = wind speed
then
(224-x) = speed against the wind
and
(224+x) = speed with the wind
:
The total time is given as 15 hrs, write a time equation: Time = Dist/speed
:
Time with + time against = 15 hrs
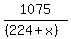 + + 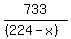 = 15 = 15
:
Multiply equation by (224+x)(224-x) to get rid of the denominators, results
:
1075(224-x) + 733(224+x) = 15(224+x)(224-x)
:
240800 - 1075x + 164192 + 733x = 15(50176 - x^2)
:
-1075x + 733x + 240800 + 164192 = 752640 - 15x^2
:
+15x^2 - 342x + 404992 - 752640 = 0; arrange as a quadratic equation
:
15x^2 - 342x - 347648 = 0
:
Solve this using the quadratic formula; a=15, b=-342, c=-347648
:
I got a positive solution (approximately): x = 164.06 is the speed of the wind
:
Checking our solution:
224 - 164.06 = 59.94 km/hr against the wind
and
224 + 164.06 = 388.06 km/hr with the wind
:
1075/388.06 + 733/59.94 =
2.77 + 12.23 = 15 hrs
|
|
|