Question 1176413: For each polynomial function, describe or determine the following, then sketch the graph.
A. Leading term
B. X-intercept
C. Y-intercept
D. Multiplicity of roots
E. Number of turning points
F. Sketch
1.y=(x^2-5) (x-1)^2 (x-2)^2
2.y=2x^4-3x^3-18x^2+6x+28
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.
 ....multiply and you will get ....multiply and you will get

A. Leading term is 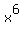
B. X-intercept are at x=sqrt(5), x=-sqrt(5),x=1,x=2
C. Y-intercept is ( , , ) )
D. Multiplicity of roots:
 Multiplicity 1 Multiplicity 1
 Multiplicity 1 Multiplicity 1
 Multiplicity 2 Multiplicity 2
 Multiplicity 2 Multiplicity 2
E. Number of turning points is 
note:
A polynomial of degree  , will have a maximum of , will have a maximum of 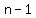 turning points. turning points.
The total number of turning points for a polynomial with an even degree is an odd number.
example: A polynomial with degree of  can have can have  , ,  , ,  , or , or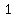 turning points turning points
The total number of points for a polynomial with an odd degree is an even number.
example: A polynomial of degree  can have can have  , , , ,  turning points (zero is an even number). turning points (zero is an even number).
F. Sketch

2.


zeros:
A. Leading term is 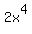
B. X-intercept are:
( ) )
(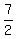 ) )
( ) )
(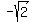 ) )
C. Y-intercept is ( , ,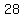 ) )
D. Multiplicity of roots
 Multiplicity of 1 Multiplicity of 1
 , Multiplicity of 1 , Multiplicity of 1
 ,Multiplicity of 1 ,Multiplicity of 1
 ,Multiplicity of 1 ,Multiplicity of 1
E. Number of turning points 
F. Sketch

|
|
|