SOLUTION: A and B are independent events. P(A|B) = 0.4. Find P(A). Round your answer to the nearest tenth.

By the definition of the conditional probability,


    P(A|B) = 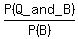.     (1)


By the definition, the events A and B are independent if 


    P(A and B) = P(A)*P(B).             (2)


By substituting (2) into (1), you have


    P(A|B) = 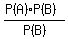 = P(A).


But P(A|B) is given: it is 0.4.


Therefore, at given conditions,  P(A) = 0.4.      ANSWER.

    for independent events A and B,  P(A|B)  does not depend on P(B) and is equal to P(A).