Question 1176218: I don't know how to do this, please!!
Newton's Law of Cooling tells us that the rate of change of the temperature of an object is proportional to the temperature difference between the object and its surroundings. This can be modeled by the differential equation dT/dt=k(T−A), where T is the temperature of the object after t units of time have passed, A is the ambient temperature of the object's surroundings, and
k is a constant of proportionality.
Suppose that a cup of coffee begins at 179 degrees and, after sitting in room temperature of 62 degrees for 11 minutes, the coffee reaches 174 degrees. How long will it take before the coffee reaches 154 degrees?
Include at least 2 decimal places in your answer.
= ? minutes
Found 2 solutions by ewatrrr, htmentor:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! dT/dt=k(T−A)
(179-174)/11=k(117)
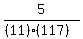 = k = .003885 = k = .003885
The temperature of an object, T, in surrounding air with temperature Ts behave according to the formula T(t)=Ae^kt+Ts
where
•t is time
•A is the difference between the initial temperature of the object and the surroundings
•k is a constant, the continuous rate of cooling of the object
154=117e^-.003885t + 62
92/117 = e^-.003885t
ln ( 92/117)/-.003885 = t = 61.875 minutes
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! The solution to the differential equation is given by:
T(t) = Ts + (T0 - Ts)exp(-kt), where Ts = the temperature of the surroundings
T0 = the initial temperature and k = the rate constant
We can use the information given to solve for k:
T(11) = 174 = 62 + (179 - 62)exp(-11k)
exp(-11k) = (174 - 62)/117 -> k = (-1/11)*ln((174 - 62)/117) = 0.0039705
You can now use this formula to solve for t, if T(t) = 154
Ans: 60.54 mins
|
|
|