Question 1176024: Evan runs a factory that makes Blu-ray players. Each T50 takes 4 ounces of plastic and 4 ounces of metal. Each G150 requires 2 ounces of plastic and 6 ounces of metal. The factory has 140 ounces of plastic, 324 ounces of metal available, with a maximum of 16 T50 that can be built each week. If each T50 generates $12 in profit, and each G150 generates $11, how many of each of the Blu-ray players should Evan have the factory make each week to make the most profit?
T50:
G150:
Best profit:
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Evan runs a factory that makes Blu-ray players. Each T50 takes 4 ounces of plastic and 4 ounces of metal.
Each G150 requires 2 ounces of plastic and 6 ounces of metal.
The factory has 140 ounces of plastic, 324 ounces of metal available, with a maximum of 16 T50 that can be built each week.
If each T50 generates $12 in profit, and each G150 generates $11, how many of each of the Blu-ray players should
Evan have the factory make each week to make the most profit?
~~~~~~~~~~~~~~~~~
Let X = # of items T50; Y = # of items G150.
From the condition, we have this formulation of maximization problem:
(1) the objective function to maximize is the profit P = 12X + 11Y dollars.
Restrictions
(2) 4X + 2Y <= 140 (plastic restriction)
(3) 4X + 6Y <= 324 (metal restriction)
(4) 0 <= X <= 16, Y >= 0.
You can make a plot of the feasibility domain.
 Plots y =
Plots y = 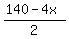 (red); y = (red); y = 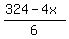 (green); x = 16 (blue)
It is a pentagon in QI adjacent to x- and y-axes, restricted by the red, the green and the blue lines.
It has vertices (X,Y) = (0,0), (0,54), (12,46), (16,38), (16,0).
The solution is one of these 5 points, where the objective function (profit) has a maximum.
The values of the function P(X,Y) at listed points are
P(0,0) = 0,
P(0,54) = 12*0 + 11*54 = 594,
P(12,46) = 12*12 + 11*46 = 650,
P(16,38) = 12*16 + 11*38 = 610,
P(16,0) = 12*16 + 11*0 = 192.
Comparing these values, you find the optimal point.
It is (X,Y) = (12,46), 12 items T50 and 46 items G150, providing maximum profit of 650 dollars. ANSWER (green); x = 16 (blue)
It is a pentagon in QI adjacent to x- and y-axes, restricted by the red, the green and the blue lines.
It has vertices (X,Y) = (0,0), (0,54), (12,46), (16,38), (16,0).
The solution is one of these 5 points, where the objective function (profit) has a maximum.
The values of the function P(X,Y) at listed points are
P(0,0) = 0,
P(0,54) = 12*0 + 11*54 = 594,
P(12,46) = 12*12 + 11*46 = 650,
P(16,38) = 12*16 + 11*38 = 610,
P(16,0) = 12*16 + 11*0 = 192.
Comparing these values, you find the optimal point.
It is (X,Y) = (12,46), 12 items T50 and 46 items G150, providing maximum profit of 650 dollars. ANSWER
Solved.
--------------
In this site, there is a lesson
- Solving minimax problems by the Linear Programming method
which explains, for beginners, metodology of solving such problems in more details.
|
|
|