SOLUTION: Tell whether each statement is sometimes, always, or never true. Explain. there are infinitely many polynomial with zeros a, b, and c

Algebra ->  Rational-functions -> SOLUTION: Tell whether each statement is sometimes, always, or never true. Explain. there are infinitely many polynomial with zeros a, b, and c      Log On


   

Question 1175934: Tell whether each statement is sometimes, always, or never true. Explain.
there are infinitely many polynomial with zeros a, b, and c
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

This statement is ALWAYS true. 

    There are INFINITELY MANY polynomials of the form


        p(x) = r*(x-a)*(x-b)*(x-c)


    with the given zeros "a", "b" and "c", where  the coefficient "r" is any real number not equal to zero.


It is one example of the infinite family of polynomials with the assigned property. 

    Also, there are INFINITELY MANY polynomials of the form


        p(x) = 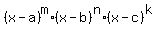%28x-a%29%5Em%2A%28x-b%29%5En%2A%28x-c%29%5Ek


    with the leading coefficient of 1 with the given zeros "a", "b" and "c", 
    where  the degree indexes n, m, k are arbitrary positive integer numbers.

It is another example.

------------

Solved, answered and explained.