Question 1175809: Find an ordered triple (x,y,z) of real numbers satisfying x<= y<= z and the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xy} + sqrt{xz} + sqrt{yz}= 30,
or, if there is no such triple, enter the word "none" as your answer.
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! ,
Find an ordered triple (x,y,z) of real numbers satisfying x<= y<= z and the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xy} + sqrt{xz} + sqrt{yz}= 30,
or, if there is no such triple, enter the word "none" as your answer.
~~~~~~~~~~~~
To simplify my writhing, I introduce new variables
a =  ; b = ; b = 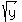 ; c = ; c =  .
Then from the given conditions, I have
a + b + c = 10 (1)
a^2 + b^2 + c^2 = 38 (2)
ab + ac + bc = 30. (3)
Square equation (1) and use this identity (a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc.
You will get then
10^2 = 38 + 2*30, or
100 = 38 + 60 = 98. (4)
Since equality (4) is IMPOSSIBLE, it means that the given system of equations HAS NO solution. .
Then from the given conditions, I have
a + b + c = 10 (1)
a^2 + b^2 + c^2 = 38 (2)
ab + ac + bc = 30. (3)
Square equation (1) and use this identity (a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc.
You will get then
10^2 = 38 + 2*30, or
100 = 38 + 60 = 98. (4)
Since equality (4) is IMPOSSIBLE, it means that the given system of equations HAS NO solution.
Proved and solved.
Explained and completed.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an ordered triple (x,y,z) of real numbers satisfying x<= y<= z and the system of equations
sqrt{x} + sqrt{y} + sqrt{z} = 10,
x + y + z = 38,
sqrt{xy} + sqrt{xz} + sqrt{yz}= 30
======================
(4,9,25) IF sqrt{xy} + sqrt{xz} + sqrt{yz}= 31
|
|
|