Question 1175742: For the given rational function f(x) = 3 - 3x over (divided by) x - 5, find the following
A) Find the intercepts for the graph.
B) Determine the domain.
C) Find any vertical or horizontal asymptotes for the graph.
D) Sketch any asymptotes as dashed lines. Then sketch a graph of y = f(x).
Homework question from Hans
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation is:
(3 - 3x) / (x - 5)
the equation will have a vertical asymptote at x = 5 because, when the value of x is equal to 5, the equation becomes -12 / 0 which is undefined.
as x approaches 5 from the left, the equation will get more and more positive.
as x approaches 5 from the right, the equation will get more and more negative.
for example, when x = 4.999, the equation becomes (3 - 3*4.999) / (4.999 - 5) = 11997 which is a positive value, and when x = 5.0001, the equation becomes (3 - 3 * 5.001) / 5.001 - 50 = -12003.
the closer you get to 5 from the left, the value of y becomes larger and larger in a positive direction.
the closer you get to 5 from the right, the value of y becomes larger andlarger in a negative direction.
the vertical asymptote ia at x = 5, where the value of y is undefined.
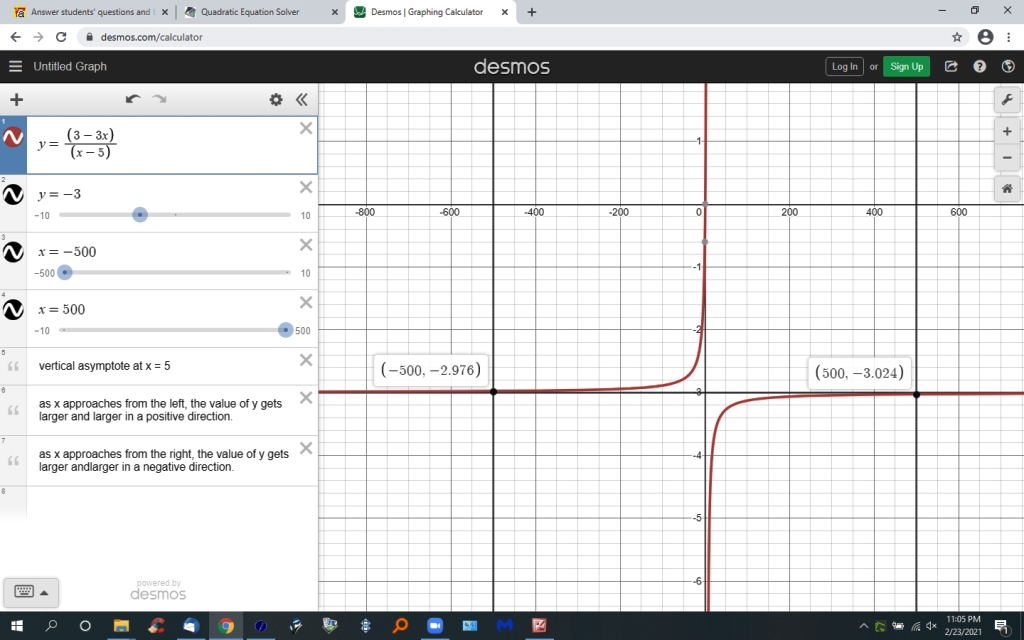
to find the horizontal asymptote, you need to let the value of x get larger and larger in both direction, i.e larger in a positive direction and larger and larger in a negative direction.
if you pick a large enough value, you will see that, as x gets larger and larger in a negative direction, y approaches the value of - 3 from a value of y that is less negative than -3, and as x gets larger and larger in a positive direction, y approaches the value of - 3 from a value of y that is more negative than -3.
for example:
when x = 100,000, the value of y is equal to (3 - 3 * 100,000) / (100,000 - 5) = -3.0001.....
when x = -100,000, the value of y is equal to (3 - 3 * -100,00) / (-100,000 - 5) = -2.99988.....
this can be seen in the following graphs.
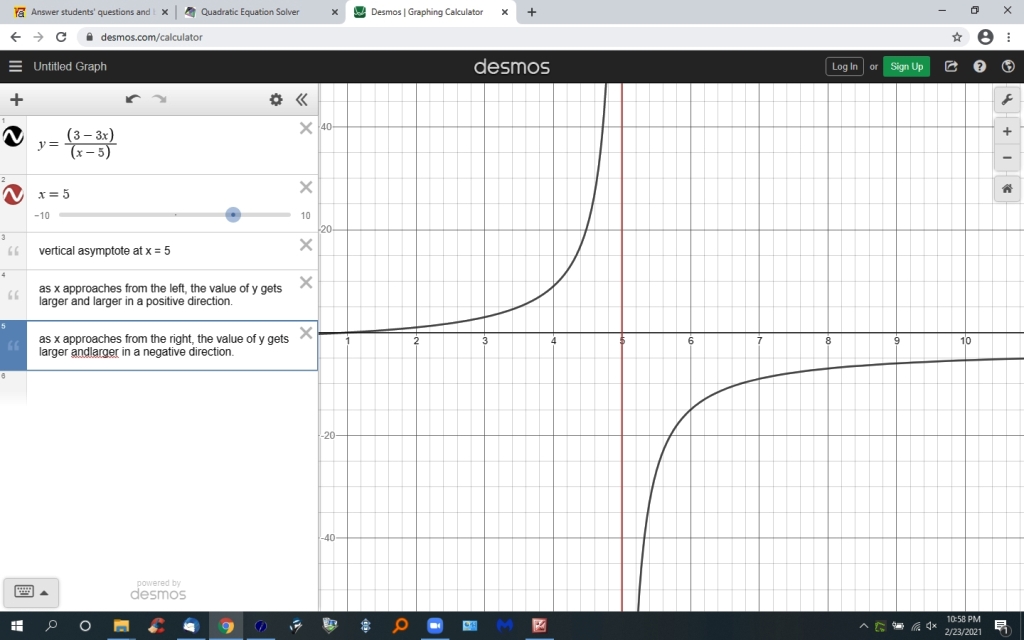
the first graph shows you the vertical asymptote at x = 5.
the second graph shows you the horizontal asymptote at y = -3.
here's a reference by purplemath.
https://www.purplemath.com/modules/asymtote.htm
there are 4 sections to that tutorial.
the first is vertical asymptotes.
the second is horizontal asymptotes.
the third is slant asymptotes.
the fourth is examples.
all are very good, but for your problem, you may want to concentrate on vertical and horizontal since your problem doesn't encounter slant asymptotes.
|
|
|