Question 1175582: A hospital administrator deposits $10,000 into an account that earns 9% annual interest compounded monthly. In approximately how many years will the investment be worth $18,000? Round to the nearest whole number.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! formula to use is f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the interest rate per time period
n is the number of time periods.
in this problem:
f = 18,000
p = 10,000
r = 9% per year divided by 12 = .75% / 100 = .0075 per month
the formula requires the rate, not the percent.
n = what you want to find.
the formula becomes:
18,000 = 10,000 * 1.0075 ^ n
divide both sides of the equation by 10,000 to get:
1.8 = 1.0075 ^ n
take the log of both sides of the equation to get:
log(1.8) = log(1.0075 ^ n)
by the law of logs that says log(x^n) = n * log(x), the equation becomes:
log(1.8) = n * log(1.0075)
divide both sides of the equation by log(1.0075) to get:
log(1.8) / log(1.0075) = n
solve for n to get:
n = 78.66508266 months.
confirm by replacing n in the original equation and solving for f.
equation becomes f = 10,000 * 1.0075 ^ 78.66508266 = 18,000.
this confirms the answer is correct.
divide the number of months by 12 to get 6.55542355 years.
round to the nearest whole number to get 7.
that's your solution.
on a graph, it looks like this.
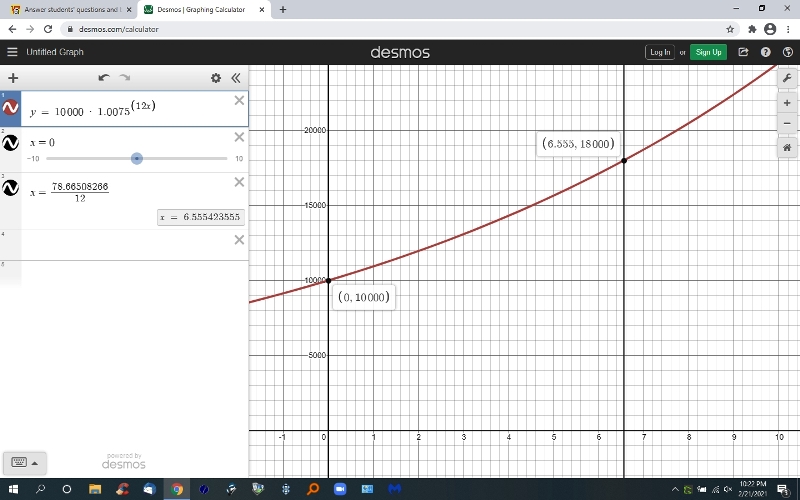
the number of years is 6.55.....
that's after the end of the 6th year which puts the solution in the 7th year.
|
|
|