Question 1175420: Suppose 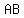 and and 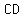 are two non-intersecting chords of a circle. Take any point are two non-intersecting chords of a circle. Take any point  on the on the
arc 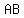 not containing not containing 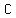 , , 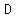 . Let . Let 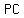 and and  intersect intersect 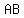 at at  , ,  respectively. Show respectively. Show
that AQ×RB/QR
is constant (irrespective of position of  ). ).
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this geometric proof step-by-step.
**Understanding the Problem**
We're given a circle with two non-intersecting chords, AB and CD. We have a point P on the arc AB (not containing C and D). Lines PC and PD intersect AB at Q and R, respectively. We need to show that the ratio (AQ * RB) / QR is constant, regardless of the position of P.
**Proof**
1. **Angles in the Same Segment:**
* ∠CPD is constant because it subtends the chord CD.
* ∠APC is constant because it subtends the chord AC.
* ∠BPD is constant because it subtends the chord BD.
2. **Similar Triangles:**
* In ΔPCQ and ΔPRB:
* ∠CPQ = ∠RPB (same angle)
* ∠PCQ = ∠PBR (angles in the same segment, subtending the arc PD)
* Therefore, ΔPCQ ~ ΔPRB (by AA similarity).
* In ΔPDR and ΔPQA:
* ∠RPD = ∠QPA (same angle)
* ∠PDR = ∠PAQ (angles in the same segment, subtending the arc PC)
* Therefore, ΔPDR ~ ΔPQA (by AA similarity).
3. **Ratios from Similar Triangles:**
* From ΔPCQ ~ ΔPRB, we have:
* PC/PR = CQ/RB = PQ/PB
* RB = (PR * CQ) / PC
* From ΔPDR ~ ΔPQA, we have:
* PD/PQ = DR/AQ = PR/PA
* AQ = (PQ * DR) / PD
4. **Express AQ * RB:**
* AQ * RB = [(PQ * DR) / PD] * [(PR * CQ) / PC]
* AQ * RB = (PQ * PR * DR * CQ) / (PD * PC)
5. **Express QR:**
* QR = PR - PQ
6. **Express the Ratio (AQ * RB) / QR:**
* (AQ * RB) / QR = [(PQ * PR * DR * CQ) / (PD * PC)] / (PR - PQ)
* (AQ * RB) / QR = (PQ * PR * DR * CQ) / [(PD * PC) * (PR - PQ)]
7. **Constant Angles and Proportions:**
* Since ∠CPD, ∠APC, and ∠BPD are constant, the ratios PD/PC, PQ/PC, PR/PD, CQ/DR, and PA/PB are also constant.
* Therefore, the product (PQ * PR * DR * CQ) / (PD * PC) is constant.
* Also, since ∠CPD is constant, then the ratio PR/PQ is constant. Then PR - PQ is proportional to PR.
* Thus (PR-PQ) is proportional to PD or PC.
* Thus the fraction (PQ * PR * DR * CQ) / [(PD * PC) * (PR - PQ)] is constant.
**Conclusion**
Since all the ratios involved are constants, the ratio (AQ * RB) / QR is constant irrespective of the position of point P on arc AB.
**Key Idea:** The proof relies heavily on the properties of angles subtended by chords in a circle and the properties of similar triangles.
|
|
|