Question 1175377: A political strategist claims that 56% of voters in Madison County support his candidate. In a poll of 200 randomly selected voters, 100 of them support the strategist's candidate. At = .05, is the political strategist's claim warranted?
1)
No, because the test value - 1.01 is in the noncritical region.
2)
No, because the test value - 2.22 is in the critical region.
3)
Yes, because the test value - 2.22 is in the noncritical region.
4)
Yes, because the test value - 1.71 is in the noncritical region.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
p = 0.56 is the claimed population proportion of people who support the candidate.
n = 200 = sample size
x = 100 = number of successes = number of people in the sample who support candidate
phat = sample proportion = estimates p
phat = x/n = 100/200 = 0.50
alpha = 0.05 = level of significance
Hypotheses:
H0: p = 0.56
H1: 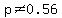
This is a two tailed test. The claim is being made in the null hypothesis (H0) since it states "A political strategist claims that 56% of voters in Madison County support his candidate".
Compute the standard error (SE)
SE = sqrt(p*(1-p)/n)
SE = sqrt(0.56*(1-0.56)/200)
SE = 0.03509985754957
Compute the test statistic
z = (phat-p)/(SE)
z = (0.50-0.56)/(0.03509985754957)
z = -1.7094086468945
z = -1.71
From this, we can immediately see that the answer must be choice (4). This is the only answer choice that has -1.71 as the test statistic.
Assuming we didn't have those answer choices, let's keep going with the problem.
We're doing a two tail test, which means that the combined area in the tails is alpha = 0.05
So that leaves an area of 1-0.05 = 0.95 in the main body between the two tails. We have a 95% confidence interval.
Use a table to determine that a 95% confidence level leads to the critical values being -1.960 and 1.960
This is the same as saying P(-1.960 < Z < 1.960) = 0.95 approximately.
The test statistic -1.71 is between the two critical values (-1.960 and 1.960) which tell us the test statistic is in the noncritical region (aka non-rejection region). Therefore, we fail to reject H0 and have no choice but to accept it. We don't have enough statistically significant evidence to overturn the null.
----------------------------------
----------------------------------
Answer: Choice 4) Yes, because the test value -1.71 is in the noncritical region.
|
|
|