Question 1175375: Can I have a detailed answer with explanations to the steps for the following question “ In a school, all of the students study physics or chemistry. Sixty percent of the students who study physics also study chemistry, but only one third of the chemistry students study physics. If there are 110 students in this school, how many of them study both of these subjects?”
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are numerous ways to set up this problem for solving. I will only show the method I would prefer to use. Probably other tutors will provide responses showing different methods.
You can look at the different methods and find one that "works" for you.
Basically, I prefer to set the problem up so that it can be solved using ratios, instead of fractions.
"60% of the students who study physics also study chemistry"
means
"3/5 of the students who study physics also study chemistry"
which means
The ratio of the number of students who take both subjects to the number who take only physics is 3:2.
NOTE: being able to convert the given fraction 3/5 into the ratio 3:2 is a useful skill that can often lead to easier ways to solve problems.
Given that 3:2 ratio....
let 3x be the number who take both subjects
let 2x be the number who take only physics
Similar reasoning tells us that "...one third of the chemistry students study physics" means that the number of students who study chemistry only is twice the number who take both subjects. (The given fraction 1/3 was converted to the ratio 1:2.)
We have 3x as the number who study both subjects, so the number who study chemistry only is 6x.
All students take one subject of the other, or both. So the sum of the numbers who take physics only, chemistry only, or both must equal the total number of students:
2x+3x+6x = 110
11x = 110
x = 110/11 = 10
ANSWER: The number of students who study both subjects is 3x = 30.
(and 20 take physics only, and 60 take chemistry only....)
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Can I have a detailed answer with explanations to the steps for the following question “
In a school, all of the students study physics or chemistry.
Sixty percent of the students who study physics also study chemistry,
but only one third of the chemistry students study physics.
If there are 110 students in this school, how many of them study both of these subjects?”
~~~~~~~~~~~~~~~~
It is a nice problem, and I will show you how to setup it.
I am sure that you NEVER saw this way to setup and will be fascinated.
The figure below shows all the class, from A to D.
P h y s i c s (from A to C)
|---------------|------------------------|---------------------|
A B C D
Both (from B to C)
C h e m i s t r y (from B to D)
Part of the class (from A to C) learns Physics.
Part of the class (from B to D) learns Chemistry.
Those in the intersection, from B to C, learn BOTH.
Let x be the unknown number of those, who learn BOTH.
Let P be the number of those who learn Physics and C be the number of those who learn Chemistry.
The problem says that 0.6P = x; hence, the number of those who learn Physics only is 0.4P.
Since 0.6P = x, it implies that 0.4P =  = = 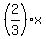 .
Next, the problem says that .
Next, the problem says that  = x; hence, the number of those who learn Chemistry only is = x; hence, the number of those who learn Chemistry only is 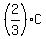 .
Since .
Since  = x, it implies that = x, it implies that 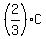 = 2x.
So, the parts are AB = = 2x.
So, the parts are AB = 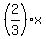 ; BC = x; and CD = 2x.
Altogether, these 3 parts comprise 110 students.
It means that ; BC = x; and CD = 2x.
Altogether, these 3 parts comprise 110 students.
It means that 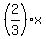 + x + 2x = 110.
At this point, the setup is done (!)
To solve this equation and to find x, multiply both sides by 3
2x + 3x + 6x = 330
11x = 330
x = 330/11 = 30.
ANSWER. 30 students study both subjects. + x + 2x = 110.
At this point, the setup is done (!)
To solve this equation and to find x, multiply both sides by 3
2x + 3x + 6x = 330
11x = 330
x = 330/11 = 30.
ANSWER. 30 students study both subjects.
Solved.
-------------
Isn't it amazing and beautiful ?
You may post me your comments, including your "THANKS" for brilliantly presented solution (!)
|
|
|