Question 1175217: Brantley and shawna walk to grandmas house at a rate of 4mi/hr. They ride their bicycles back at 8 mi/hr over the same route that they walked, it takes 1hr longer to walk then ride. How long did it take them to walk to grandmas
Found 3 solutions by Boreal, ikleyn, greenestamps:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! x hours walking, x-1 hours riding
distance is the same=velocity*time
4x=8(x-1)=8x-8
4x=8
x=2 hours walking there
x-1 hour riding back
It took them 2 hours.
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let t be the time walking to grandma, in hours
Then the time riding back is (t-1) hours, according to the problem.
The distance is the same for both routes, so you write this distance equation
4t = 8*(t-1).
Next you simplify and solve it
4t = 8t - 8
8 = 8t - 4t
8 = 4t
t = 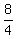 = 2 hours. ANSWER = 2 hours. ANSWER
Solved.
It was formal algebra solution.
You can solve the problem MENTALLY, too.
The speed back is twice the speed going there.
So, the time going there is twice the time going back.
The difference of these times is 1 hour.
So, the longer time is 2 hours.
You get the same answer.
Solved (in 2 ways).
---------------
Post solution note added after reading the post by @greenestamps.
My approach to teaching in this web-site / (forum) is different from that of @greenestamps.
My starting point is that the students come to this forum to get help in Algebra -
they want FIRST to be TOUGHT in Algebra.
So my first intention and my first concern is to present them an Algebra solution and Algebra approach.
After that, when it is appropriate, I give them a mental solution by reasoning.
It is NOT ALWAYS appropriate to combine both approaches in one post.
The "golden rule" of good teachers is: tell students TRUTH and ONLY TRUTH, but not "all the TRUTH" at once.
Not "all the TRUTH" at a time.
All the truth should go to students gradually with time
(and according with their ability to absorb this truth)
and "by parts".
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Pay attention to the response from tutor @ikleyn, in which she shows an informal solution in addition to a formal algebraic solution.
The process for solving the problem using formal algebra is well defined. Solving the problem by that method will not require a lot of thinking -- you just follow the well-defined algebraic steps.
On the other hand, solving the problem informally, by using logical reasoning and mental arithmetic, will give you MUCH BETTER exercise for your brain. That mental exercise will help prepare you for solving problems in the future -- not only in mathematics, but in life in general.
So when you see a problem like this, before you plunge into a solution using formal algebra, give yourself the benefit of taking a few moments to try reasoning out a solution informally.
|
|
|