SOLUTION: Can anyone solve this? f(x)=x^4-8x^3+22x^2-24x+7

It make no sense to say "solve" here.  What did the book ask you to do?
Did it say "Find the zeros"?  Did it say factor? Did it say graph? Did
it ask for the degree?  Did it ask for the multiplicities of the zeros?

We can't help you without the instructions, and "solve" is not the
proper instructions for this problem.  What are the instructions?

Edwin

No, Ikleyn, this student wrote me this in his "thank-you" letter.

This student apparently is studying very complicated algebraic factoring
methods.

The quartic is factorable algebraically using radicals (square roots):



We try to reduce it to a quadratic in y², by substituting a linear form for x,
say x=ay+b



We see if we can choose "a" and "b" so that the terms in y³ and y become 0.

It isn't difficult to see that the only two terms in y³ are

4a³by³ - 8a³y³ = 4a(b-2)y³, which would be 0 for all y if b=2

There are four terms in y, and they are

4ab^3y - 24 ab^2y + 44aby - 24ay

Substituting b=2

32ay - 96ay + 88ay - 24ay which, luckily, equals 0

Therefore, we can simply take a = 1, and b = 2

Then x = ay+b = y+2



becomes



which simplifies to



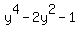and by the quadratic formula,



So there are two real zeros for y

, 

And there are two imaginary zeros for y

, 

Since √2 is greater than 1,

, 

So the factorization in terms of y is:



Since x = y+2, we substitute x-2 for y



Edwin